很神奇的, 使用了RBF但是速度却不快(

A Three-Level Radial Basis Function Method for Expensive Optimization

TLRBF 用于昂贵优化的三层径向基函数方法

本文提出了一种三层RBF（TLRBF）辅助的优化算法来处理昂贵优化的问题。更具体地说，为了整合整个搜索空间的粗粒度全局搜索（GS）、有希望的子区域的中粒度子区域搜索（SS）和最有希望的局部区域的细粒度局部搜索（LS），在TLRBF的每个迭代中，分别产生三种解决方案供GS、SS和LS评估。在GS中，所有可用的解决方案被用来构建一个全局RBF近似函数，然后使用随机抽样方法来提供一个新的解决方案，该解决方案具有良好的目标函数值，并与先前评估的解决方案保持一定的距离。在SS中，由模糊聚类确定的可用解决方案的一个子集被用来训练一个子区域RBF近似函数，然后由优化器对其进行优化，以找到其最佳的精确评价。在LS中，当前的最佳解决方案和它的邻居被用来建立一个局部的RBF近似函数，该函数也被一个优化器最小化，以找到其最佳评估。

背景知识

RBF 径向基函数

所谓径向基函数，其实就是某种沿径向对称的标量函数。通常定义为空间中任一点x到某一中心c之间欧氏距离的单调函数，可记作φ(||x-c||)，其作用往往是局部的，即当x远离c时函数取值很小

如高斯径向基函数：RBF(x,c)=exp(−(x−c)2r2)RBF(x,c)=exp\left( - \frac{(x-c)^2}{r^2}\right)

径向基函数的诞生主要是为了解决多变量插值的问题,比如下图:

img

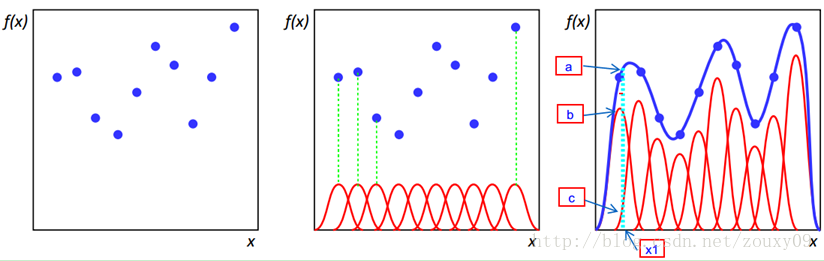
左图中每个蓝色的点是一个样本.在每个样本上面放一个基函数,如中间图,绿色虚线表示的是每个训练样本对应的一个径向基函数（以高斯函数为例),样本点也叫中心(center)点

假设真实函数曲线是蓝色的那根（最右边的图），如果我们有一个新的数据x1，我们想知道它对应的f(x1)是多少，也就是a点的纵坐标是多少。那么可以看到，a点的纵坐标等于b点的纵坐标加上c点的纵坐标。而b的纵坐标是第一个样本点的径向基函数的值乘以一个大一点的权值得到的，c的纵坐标是第二个样本点的径向基函数的值乘以另一个小点的权值得到。而其他样本点的权值全是0，因为我们要插值的点x1在第一和第二个样本点之间，远离其他的样本点，那么插值影响最大的就是离得近的点，离的远的就没什么贡献了。所以x1点的函数值由附近的b和c两个点就可以确定了。拓展到任意的新的x，这些红色的径向基函数乘以一个权值后再在对应的x地方加起来，就可以完美的拟合真实的函数曲线了。

总结就是，RBF根据某种距离来描述点与某个中心点的的相似度

规范定义

RBF插值模型可以表示为

S(x)=∑k=1Kwkϕ(∥x−xk∥)S(\mathbf{x}) = \sum_{k = 1}^{K} w_{k} \phi\left(\left\|\mathbf{x}-\mathbf{x}_{k}\right\|\right)

W = (w1, w2,..., wK)T是权重向量,φ就是基函数.一组中心点{x1, x2,..., xK}组成训练数据集D={(xi, f(xi)), i = 1, 2,..., N}，其中N是训练数据集的大小。

为了算出权重向量W，应该满足以下插值条件(就是上面说的用多组基函数拟合中心点):

S(xi)=f(xi)S\left(\mathbf{x}_{i}\right)=f\left(\mathbf{x}_{i}\right)

可以用矩阵形式写成:

ΦW=f\mathbf{\Phi} \mathbf{W}=\mathbf{f}

Φi,j=ϕ(∥xi−xj∥)\boldsymbol{\Phi}_{i, j}=\phi\left(\left\|\mathbf{x}_{i}-\mathbf{x}_{j}\right\|\right) , f=[f(x1),f(x2),...,f(xn)]T

通过解决线性方程组，可以得到权重向量W，即 W=(ΦTΦ)−1ΦTf\mathbf{W}=\left(\boldsymbol{\Phi}^{T} \boldsymbol{\Phi}\right)^{-1} \boldsymbol{\Phi}^{T} \mathbf{f}

在这篇文章中，采用了以下的多元函数作为基函数:

ϕ(r)=r2+δ2\phi(r)=\sqrt{r^{2}+\delta^{2}}

δ是基函数的形状参数

最后，对于一个新的输入x∗，其预测的输出可以用下式计算:

S(x∗)=∑k=1Nwkϕ(∥x∗−xk∥)S\left(\mathbf{x}^{*}\right)=\sum_{k=1}^{N} w_{k} \phi\left(\left\|\mathbf{x}^{*}-\mathbf{x}_{k}\right\|\right)

常见的基函数

径向基函数有几类，如高斯函数、立方样条、线性样条等(Gaussian function, cubic spline, and linear spline)

立方样条曲线在小的计算预算下具有优异的性能,其表达式 $ \phi\left(\left|\mathbf{x}-\mathbf{x}{i}\right|\right)=\left(\left|\mathbf{x}-\mathbf{x}{i}\right|\right)^{3} $

所提算法

算法涉及三种"搜索":

粗粒度全局搜索（GS）:它可以探索不同的下层盆地，以避免陷于局部最优区域

中粒度子区域搜索（SS）:它可以利用已经发现的有希望的盆地，以确定哪一个盆地是最有希望的。

细粒度局部搜索（LS）:它可以有效地开发最有潜力的盆地

人话:一个函数可能有多个不同的深坑,GS找出深坑,SS找出坑深的部分,LS找出该部分的最深处

GS、SS和LS协同工作，可以实现探索和开发之间的良好平衡。

首先介绍所提出的TLRBF算法的总体框架，然后详细介绍GS、SS和LS

总体框架

image-20220607163813450

一开始，一组初始样本(作为中心点)xInit = {x1, x2, . . . , xn0}通过某种方法在整个搜索空间Ω产生，n0是初始样本的数量。本文采用拉丁超立方体抽样（LHS）方法产生初始样本，然后，初始训练数据集DI = {（xi, fi）, i = 1, 2, . ，n0}。初始化后，该算法迭代更新D，直到满足停止标准。

在每一次迭代中:

在全局层面，利用数据库D构建一个全局RBF模型SG(x)。基于SG(x)，GS在整个搜索空间中搜索一个有希望的、未开发的解决方案xG，进行昂贵的评估。

在中等水平上，根据模糊聚类选择当前数据库D的一个子集DS，并建立一个子区域RBF模型SS(x)。基于SS(x)，SS通过在子搜索空间中最小化SS(x)找到一个有希望的解决方案xS。

在局部层面上，当前的最佳解xb及其k个最近的邻居(KNN)被用来建立局部RBF模型SL(x)，并通过在相应的LS空间中优化SL(x)得到新的解xL。当满足停止标准时，数据库D中的最佳解xb将成为最终解。

本文使用Jade作为优化器来求解SS和LS的次优化问题

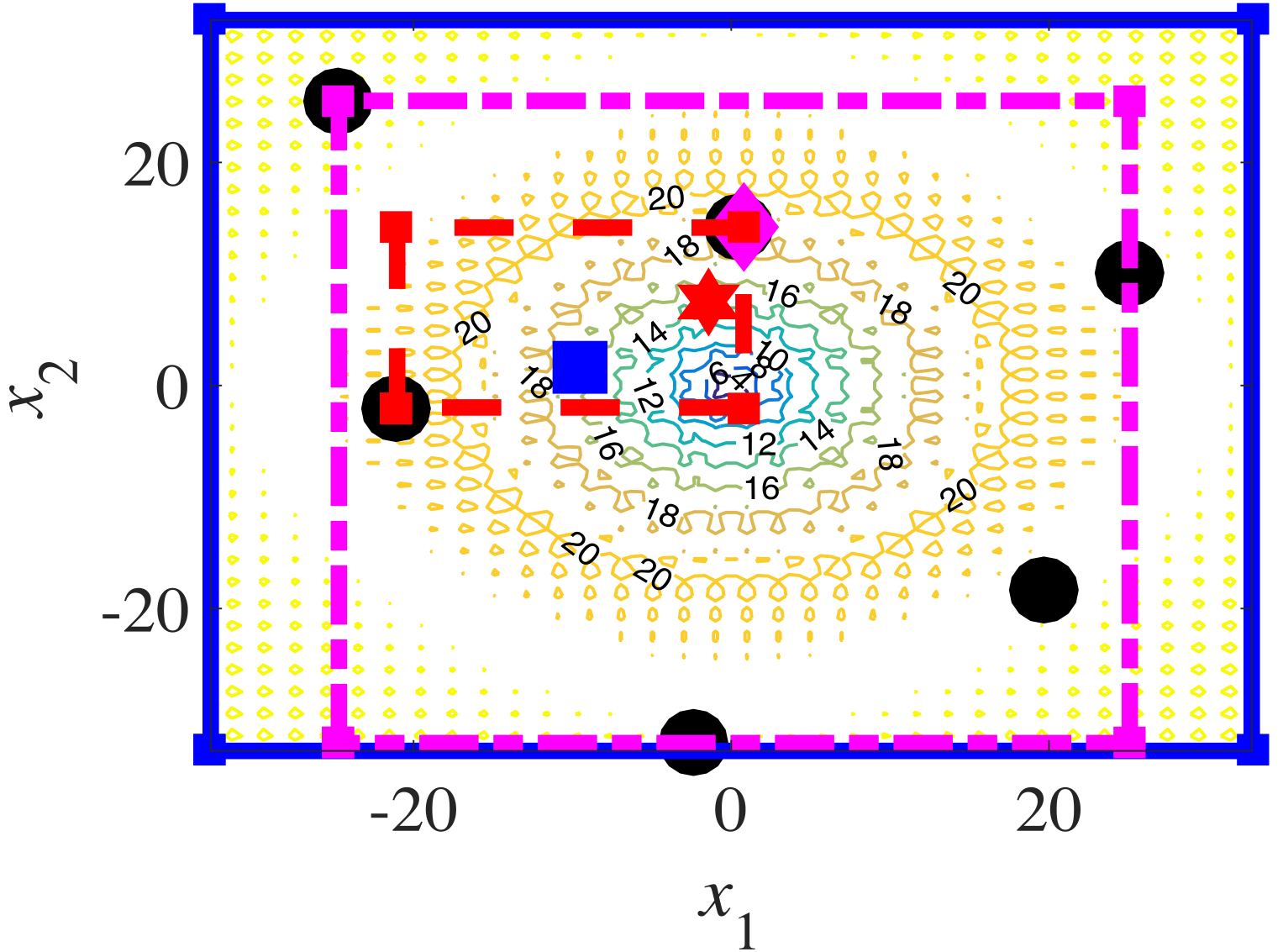
image-20220607165557308

上图显示了TLRBF在椭球问题(d=2)的一次迭代中的搜索过程。蓝色实心框、品红色点划线框和红色虚线框分别表示GS区域、SS区域和LS区域。在一次迭代中，GS、SS和LS分别在整个搜索空间、一个子区域和一个局部区域生成三个解。黑点是之前评估过的解决方案。蓝色正方形点、洋红色菱形点和红色六角星点分别由GS、SS和LS生成。

下图以另一个视角呈现不同的搜索范围:

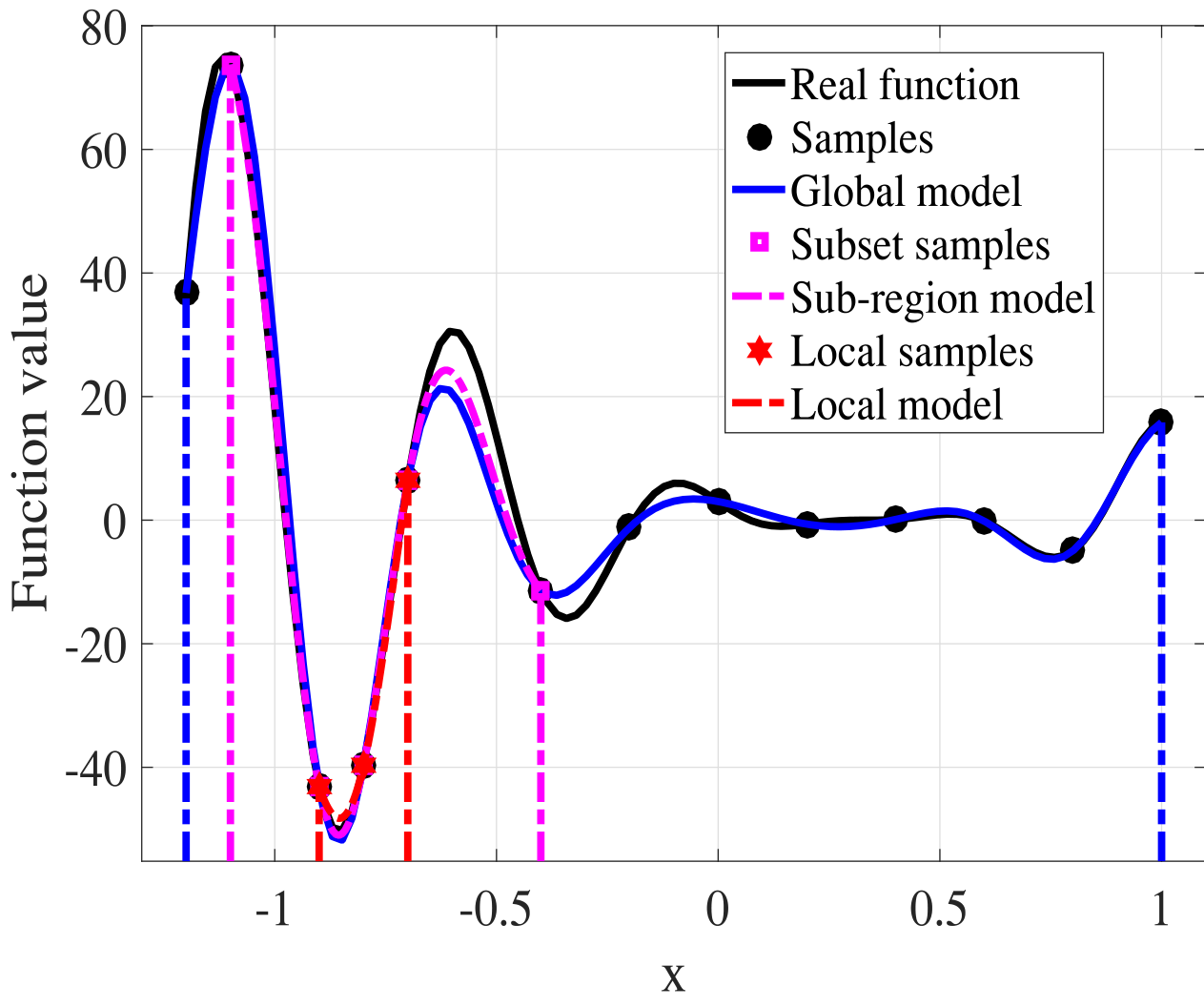
image-20220607172619991

整个搜索空间为Ω = [-1.2, 1]，子区域为ΩS = [-1.1, -0.4]，局部区域为ΩL= [−0.9, −0.7]

全局搜索GS

GS专注于探索整个搜索空间中尚未开发和有前途的领域Ω,使用所有可用解来构造全局代理模型SG(X)，以刻画整个适应度概览。

基于全局模型和评估点，新的解xG被确定如下：(解是一个集合,不只是一个点)

xG=arg⁡min⁡y∈BSG(y)B={y∣y∈A,min⁡x∈D∥y−x∥>αΔG}\begin{aligned} \mathbf{x}^{G} &=\underset{\mathbf{y} \in \mathbf{B}}{\arg \min } S_{G}(\mathbf{y}) \\ \mathbf{B} &=\left\{\mathbf{y} \mid \mathbf{y} \in \mathbf{A}, \min _{\mathbf{x} \in \mathbf{D}}\|\mathbf{y}-\mathbf{x}\|>\alpha \Delta_{G}\right\} \end{aligned}

其中，A = {y1, y2, . . . , ym}是一个大的样本集，在搜索空间Ω中均匀地随机生成(和中心点集不是一个东西)

B是A的一个子集，只包括A中满足距离约束的样本；D是当前的数据库，由所有先前评估的点组成；ΔG = maxy∈Aminx∈D||y - x||是最大距离约束,0 ≤ α < 1是比例因子

大概的例子:

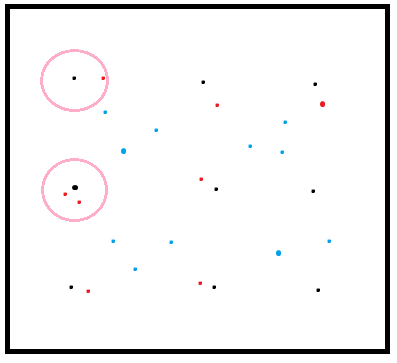
image-20220607212403436

黑色是中心点,粉色圈是距离约束,红色和蓝色点组成A.圈内的红色点由于里中心点太近从而不采用,而蓝色的点都不在粉圈内,符合要求,会纳入B中

这种填充式采样策略的好处是。1）均匀生成的样本集A对任何搜索区域都没有偏见；2）xG很可能是一个有希望的区域，因为它是基于代理模型的一大批均匀点中最好的一个集合；3）xG在下一次迭代中可能对提高模型质量有用，因为它处于可用信息很少的区域。算法2中提供了GS的伪代码。

image-20220607171255351

在GS中，需要产生一大组样本来覆盖整个搜索空间。随机均匀抽样或者其他一些方法(如LHS)都可以用于这个目的。然而，我们的实验结果表明，采样策略对所提算法的性能并不关键。因此在实验中采用随机均匀抽样方法。

子区域搜索SS

子区域模型在子区域内可以获得与全局模型相似的近似精度,子区域模型可以像全局模型一样指导ΩS中的优化工作。通过子区域划分，计算资源可以得到合理的分配。

在中等水平上，由当前数据库D的一个子集DS构建的子区域RBF模型SS(x)被用来开发相应的有希望的子区域。

本文采用了模糊c均值聚类(fuzzy c-means algorithm, FCM).它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而决定样本点的类属以达到自动对样本数据进行分类的目的

首先，为了确定聚类的数量，采用了两个控制参数L1和L2。L1表示每个簇的最大点数，L2表示再增加一个所要的点的数量。基于L1和L2，聚类的数量计算如下(9)

c=1+max⁡{0,[N−L1L2⌉}c=1+\max \left\{0,\left[\frac{N-L_{1}}{L_{2}}\right\rceil\right\}

其中N是先前评估的点的数量。如果N≤L1，c=1就意味着所有样本都被归入同一个聚类，即DS=D。如果N>L1，那么N个点通过模糊c-means聚类被分成c个聚类。每个聚类Cj, j = 1, 2,...,c 包括对自身具有最高成员度的L1点。此外，当N>L1和L1>L2时，由于c-L1>N，不同的聚类共享一些共同点。

聚类后，用一个聚类中所包含的点的平均目标函数值来代表这个聚类的质量，其计算公式为(10)

Qj=∑x∈Cjf(x)L1,j=1,2,…,cQ_{j}=\frac{\sum_{\mathbf{x} \in \mathbf{C}_{j}} f(\mathbf{x})}{L_{1}}, \quad j=1,2, \ldots, c

然后，根据集群的质量Q，以升序进行排序，接着将每个集群的等级分配为rj = c - Ij + 1 . Ij是排序后第j个簇的索引

pj=rjc,j=1,2,…,cp_{j}=\frac{r_{j}}{c}, \quad j=1,2, \ldots, c

最后，可以根据选择概率pj选择一个集群来确定子集DS。然后，可以使用子集DS来训练一个子区域RBF模型SS(x)。最后，填充采样策略被定义为(13)

xS=arg⁡min⁡x∈ΩSSS(x)\mathbf{x}^{S} =\underset{\mathbf{x} \in \Omega_{S}}{\arg \min } S_{S}(\mathbf{x})

image-20220607174857626

如果解决方案xS过于接近先前评估的点(不满足19行)，xS将被直接删除。

综上所述，SS的优点有以下几点。1）模糊聚类能够将整个搜索空间分割成多个重叠的平衡子区域，这样可以提高边界区域的近似精度；2）更好的子区域具有更高的利用概率，这自然能够导致探索和利用之间的良好平衡；3）下一个代理模型的xS周围的近似质量将得到改善，这为在接下来的迭代中利用xS周围的区域带来机会。

初步的实验结果表明，模糊c-means聚类总是比k-means聚类好。原因可能是模糊c-means聚类比k-means聚类能将整个搜索空间划分为更均衡的子区域，而且模糊c-means聚类得到的重叠结构能更有效地利用现有数据

局部搜索LS

LS专注于利用当前最佳解xb周围最有希望的局部区域，其目的是完善迄今为止发现的最佳解。为此，应首先确定xb周围的一组局部训练点DL。本文采用KNN方法来确定DL，即

DL=(xb,f(xb))∪(xin,f(xin))\mathbf{D}_{L}=\left(\mathbf{x}_{b}, f\left(\mathbf{x}_{b}\right)\right) \cup\left(\mathbf{x}_{i}^{n}, f\left(\mathbf{x}_{i}^{n}\right)\right)

(xni,f(xni)), i = 1,2,...,k，是当前最佳解xb的k个最近的邻居

在获得本地训练数据集DL后，建立一个本地RBF模型SL(x)。LS的目标是在相应的局部区域找到SL(x)的最优解，即

xL=arg⁡min⁡x∈ΩLSL(x)\mathbf{x}^{L} =\underset{\mathbf{x} \in \Omega_{L}}{\arg \min } S_{L}(\mathbf{x})

image-20220607205603638

算法4中给出了LS的伪码。同样，只有在满足距离约束(第6行)的情况下，才能对得到的xL进行评估，其中ΔL也是一个小的正常数。

在SS和LS中，采用ΔS和ΔL来保持解决方案的多样性。L应该小于S

实验

测试函数

image-20220608135353535

六种TLRBF的变体，包括三种单级变体和三种双级变体，即TLRBF-G、TLRBF-S和TLRBF-L，分别表示TLRBF只应用GS、SS和LS；TLRBF-GS、TLRBF-GL和TLRBFSL分别表示TLRBF进行GS和SS、GS和LS、SS和LS。

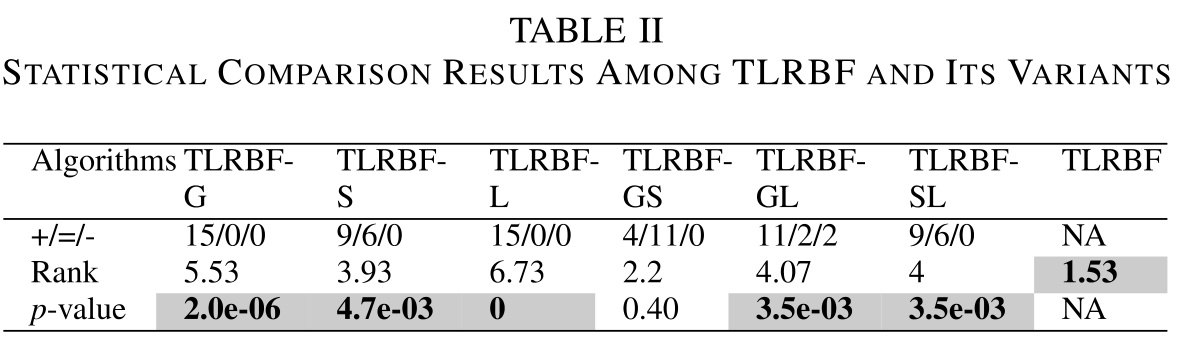
image-20220608135516270

如表二所示，TLRBF明显优于所有单层变体和两层变体（TLRBF-GL和TLRBF-SL）

SS在TLRBF中起着最重要的作用，因为TLRBF-S优于TLRBF-G和TLRBF-L，而且包括SS在内的变体（TLRBF、TLRBF-GS、TLRBF-S和TLRBF-SL）往往优于其他（TLRBF-G、TLRBF-L和TLRBF-GL）。原因可以解释为，单一的GS过度关注探索，而单一的LS主要关注开发，而SS能够在未开发区域的探索和有前景区域的开发之间获得相对平衡。

每种成分都对TLRBF的性能做出了贡献，因为TLRBF优于其他任何组合

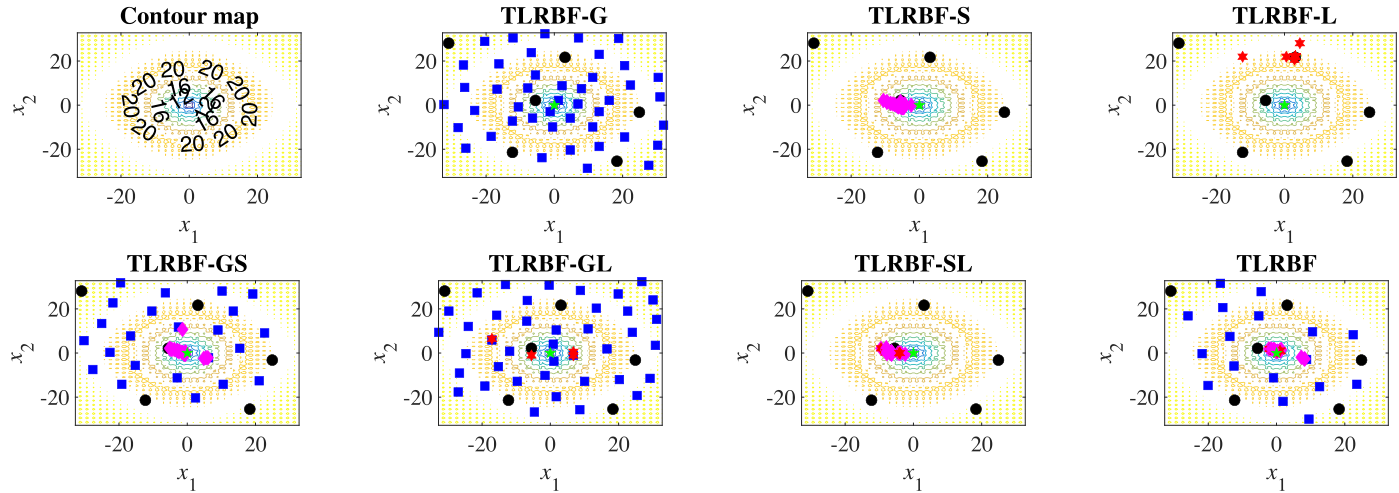
image-20220608140451389

上图显示了TLRBF及其变体在Ackley函数（d=2）上得到的50个解决方案的散点图。所有方法都从相同的初始样本开始。

对于单级方法，TLRBF-G获得的解几乎覆盖了整个搜索空间，而对于TLRBF-S和TLRBF-L，它们的解覆盖了一些不包括全局最优的小子区域

对于两级方法来说，TLRBF-GS和TLRBF-GL的解决方案的分布与TLRBF-G类似。然而，TLRBF-GS可以在SS的帮助下定位全局最优区域。对于TLRBF-SL来说，其解决方案集中在一个小的子区域。但是，他们并没有集中在全局最优区域。而对于TLRBF来说，其解决方案分散在比TLRBG-G、TLRBG-GS和TLRBF-GL更小的区域

而TLRBF有更多的解决方案落入全局最优区域。从直观上看，TLRBF在定位全局最优方面比其他变体更好。

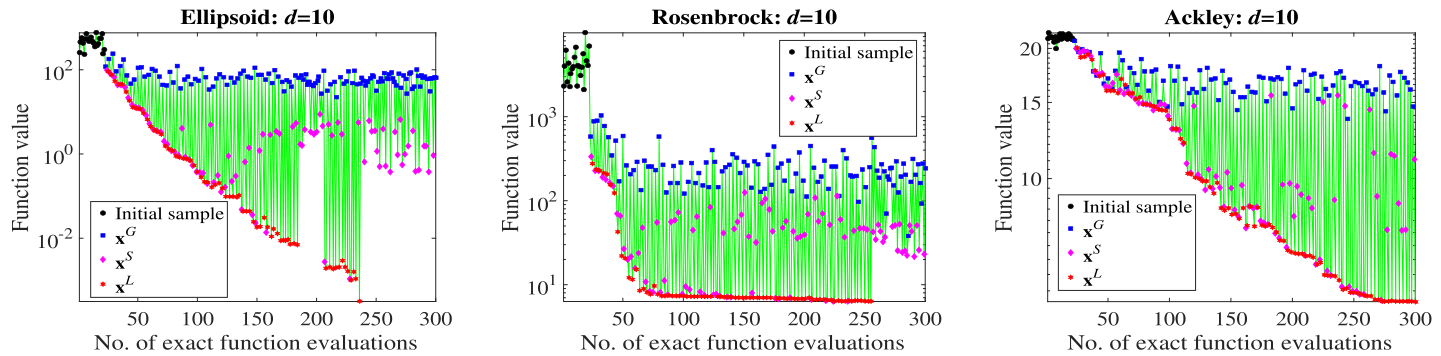
image-20220608141402069

上图绘制了GS、SS和LS在优化过程中产生的解决方案的质量，这三个代表性的函数（d = 10）。一般来说，我们可以发现，xS比xG好，xL比xS好。需要指出的是，尽管每次迭代的最佳解总是由LS产生的，但这并不意味着GS和SS是无用的，因为LS在没有GS和SS的帮助下表现得很差。

image-20220608141914237

为了研究GS、SS和LS对最佳解xb的改进有多少次贡献，在上图中统计了GS、SS和LS的平均调用次数，以及它们相应的成功调用次数。如图所示，GS的平均成功率（成功率指平均成功调用次数除以平均调用次数）小于SS，SS的平均成功率小于LS。

这一现象也说明了。1）GS负责探索整个搜索空间，所以很难直接改进xb；2）SS侧重于利用一些有希望的子区域，所以相对来说更容易找到比xb更好的解决方案；3）LS负责利用目前找到的最佳解决方案的邻域，所以最容易对xb进行改进。

总结

在这篇文章中，我们提出了一种TLRBF辅助的算法，用于解决昂贵的优化问题。它由GS、SS和LS组成。GS是寻找未开发的和有希望的子区域，SS是识别最有希望的子区域，而LS则是利用目前发现的最佳局部区域。TLRBF处理黑匣子昂贵的优化问题的性能已经被一些数值实验所验证。实验结果证实了我们的设计原则，即GS、SS和LS相互补充，它们的合作可以在有限的函数评估数量内保持探索和利用之间的良好平衡。

如何自适应地将函数评估分配给GS、SS和LS是我们未来工作中的一个重要研究问题。此外，我们将研究模型层的数量与问题复杂性和维度之间的相关性，并探索使用三层以上的模型是否能进一步改善我们的方法。我们还计划使用我们提出的方法来解决一些现实世界中昂贵的优化问题