TLDR: Sunday算法是一种比KMP算法简单且更快的字符串匹配算法.尽管如此,由于种种原因,目前更通用的算法是BM算法
字符串匹配,是在一个字符串s中寻找与子串(也称模式串,pattern,简称p)首次匹配的索引位置.解决这个问题最简单的方法肯定是暴力搜索,套2个for循环去遍历.然而这样做的时间复杂度是O(m*n),m是s的长度,n是p的长度.如果想要更高效的做法,很多书/网站会介绍KMP算法,它的复杂度是O(m+n).然而KMP算法的做法比较复杂,特别是那个next数组,我也整不明白(.然后我偶然看到了一个叫Sunday的算法,它也是用来做字符串匹配的,但是实现简单得多,而且它居然比KMP还快,平均时间复杂度降低到了O(m/n).所以不会KMP也没关系,学个Sunday也不错(
Sunday算法
Sunday算法比KMP,BM算法出现的晚(1990年),它是对BM算法的进一步小幅优化
流程演示
先不讲实现,我们先看看Sunday算法是怎么做的:
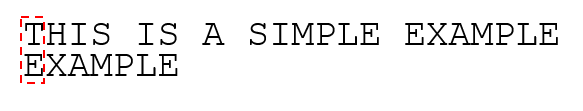
首先原字符串和子串左端对齐,发现“T”与“E”不匹配之后,检测原字符串中下一个字符(在这个例子中是“THIS IS”后面的那个空格,索引为7)是否在子串中出现,如果出现移动子串将两者对齐,如果没有出现则直接将子串移动到下一个位置。这里空格没有在子串中出现,移动子串到空格的下一个位置“A”:

发现“A”与“E”不匹配,但是原字符串中下一个字符“E”(索引15)在子串中出现了,第一个字符和最后一个字符都有出现,那么移动子串靠后的字符与原字符串对齐:

然后发现空格和“E”不匹配,原字符串中下一个字符“空格”也没有在子串中出现,所以直接移动子串到空格(索引16)的下一个字符“E”(索引17):
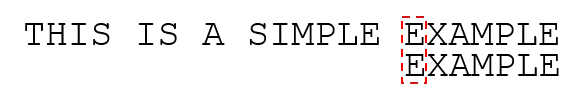
这样从头开始逐个匹配,匹配成功!
算法解释
Sunday算法是从前往后匹配,如果匹配失败,关注的是主串中参加匹配的最末位字符的下一位字符,对此有两种情况:
- 如果该字符没有在模式串中出现则直接跳过,即移动位数 = 模式串长度 + 1(即全部不匹配,整个挪走)
- 否则,其移动位数 = 模式串中该字符最右出现的位置到尾部的距离 + 1 = 模式串长度 - 该字符最右出现的位置(以0开始)
对于第二种情况的移动位数,我们可以预先用哈希表计算并存起来,代码也很简单
def calc_shift_dict(pattern:str) -> dict[str, int]:
shift_dict={}
for i, c in enumerate(pattern):
shift_dict[c] = len(pattern) - i
return shift_dict
# 以 'EXAMPLE' 为例
# shift_dict = {'E': 1, 'X': 6, 'A': 5, 'M': 4, 'P': 3, 'L': 2}
# 循环中,最后一个E会更新第一个E的值,以达到最右出现的位置的效果
有了这个偏移表,后续逻辑写起来就很容易了,比KMP简单的不是一点半点:
def sunday(s: str, p: str) -> int:
n, m = len(s), len(p)
shift_dict = calc_shift_dict(p) # 生成偏移表
i = 0
while i + m <= n: # 以免 s[i: i + m] 超出范围
if s[i: i + m] == p:
return i # 匹配完成,返回模式串 p 在文本串 s 的位置
if i + m == n: # 边界情况: 匹配到 s 末尾了,不能再取末尾的下一个索引了
return -1
i += shift_dict.get(s[i + m], m + 1) # 通过偏移表,向右进行进行快速移动
return -1 # 匹配失败
这里最脑梗的就是第8行的if,你也许会想,我直接while改成while i + m < n,然后不就可以去掉if i + m == n这个判断了?
然而不行,因为while是来判断取s的切片有没有超出s的长度,而if是来判断模式串末尾是不是移动到了s的末尾
举一个例子: s和t都是'abc',那么一开始i + m = 0 + 3 = 3跟n是一样的,这会导致进不去while而返回-1,然而真实结果应该是0,所以while不能修改
那if能不能单去掉?也不能,考虑s='abc' t='abd',一开始可以进入while,然后第一个if不行,如果没有第二个if,那就到了shift_dict.get(s[i + m], m + 1)这里,由于s最大索引是2,但是i + m是3,这样就会超出索引报错.第二个if就是为了兜住这个边界情况而存在的
优缺点
Sunday算法的优点:
- 匹配逻辑简单,比较符合直觉;写起来也简单,只需要注意最后匹配到末尾的边界情况就行了
- 预处理时间较短,大部分情况也比KMP快,平均时间复杂度是O(n/m)
很可惜,这么简洁的算法却没有BM算法流行,因为它也有软肋:
- Sunday算法的核心依赖于偏移表,而偏移表的值则取决于模式串,那么就可能存在模式串构造出很差的偏移表,比如
aaaaa的表就是{a:1},这导致每次匹配失败时,只让模式串向后移动一位再进行匹配。这样就让Sunday算法的时间复杂度飙升到了O(m*n),也就是字符串匹配的最坏情况
根据知乎该位用户所言,Sunday算法有比较高的可能达到最坏时间复杂度

那么不同的适用于哪里呢?我为此请教了ChatGPT(
Q: BM算法和Sunday算法 实际中哪个更常用? 为什么?
A: BM算法和Sunday算法都是常见的字符串匹配算法,但它们在实际中的使用情况会因为具体的应用场景而有所不同。
BM算法是一种高效的字符串匹配算法,它的时间复杂度是O(n/m),其中n和m分别是文本串和模式串的长度。BM算法在大部分情况下都比Sunday算法更快速,因此在需要高效匹配的场景中,如文本编辑器、搜索引擎等领域,BM算法被广泛使用。
Sunday算法是一种比较简单的字符串匹配算法,它的时间复杂度也是O(n/m),但是它的实现比BM算法要简单得多。Sunday算法主要适用于模式串比较短的情况,当模式串长度小于等于20时,Sunday算法的表现往往比BM算法更好,因为它的预处理时间较短,可以更快地生成偏移表
因此,BM算法在大部分情况下更常用,特别是在需要高效匹配的场景中。但在模式串较短的情况下,Sunday算法可以提供更快的匹配速度
Q: 那KMP算法呢?
A: KMP算法也是一种常见的字符串匹配算法,它的时间复杂度也是O(n+m)。
与BM算法和Sunday算法不同的是,KMP算法使用一个next数组来预处理模式串,从而实现快速匹配。具体来说,KMP算法预处理出模式串的next数组后,在匹配过程中,利用next数组中存储的信息来跳过一些不必要的比较,从而提高匹配效率。
KMP算法适用于文本串和模式串长度相近或者模式串长度较短的情况下,它在一些场景下比BM算法和Sunday算法更适合。例如在字符串匹配长度较短的情况下,KMP算法的预处理时间相对较短,因此在这种情况下,KMP算法可以比BM算法更快地进行匹配。
综上所述,KMP算法也是一种常见的字符串匹配算法,在某些情况下可以比BM算法和Sunday算法更适合。但在需要高效匹配的场景中,BM算法的效率往往更高一些。
所以实际中是BM算法用得更多,事实上,各种记事本的“查找”功能(CTRL + F)一般都是采用BM算法
其他字符串匹配算法简介
暴力算法
暴力检索法是最好想到的算法,也最好实现,在情况简单的情况下可以直接使用:
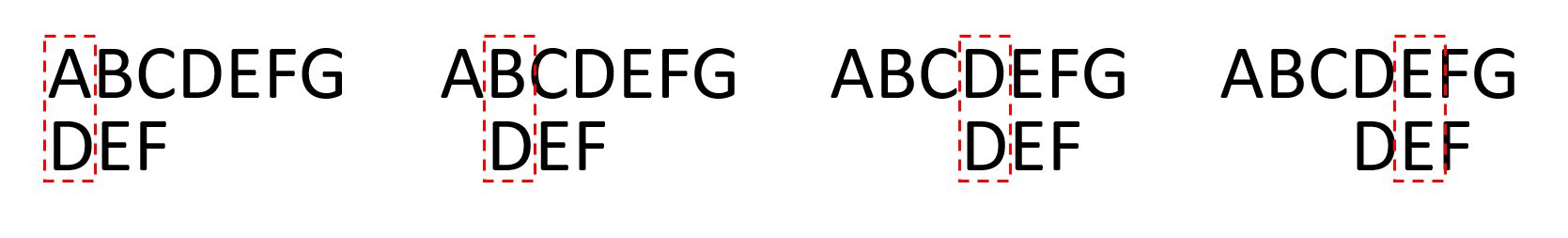
首先将原字符串和子串左端对齐,逐一比较;如果第一个字符不能匹配,则子串向后移动一位继续比较;如果第一个字符匹配,则继续比较后续字符,直至全部匹配。
时间复杂度: O(m*n)
RK算法
RK算法是对BF算法的一个改进:在BF算法中,每一个字符都需要进行比较,并且当我们发现首字符匹配时仍然需要比较剩余的所有字符。而在RK算法中,就尝试只进行一次比较来判定两者是否相等。
RK算法也可以进行多模式匹配,在论文查重等实际应用中一般都是使用此算法。
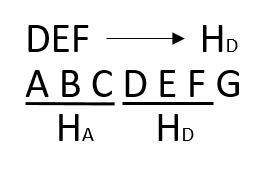
首先计算子串的HASH值,之后分别取原字符串中子串长度的字符串计算HASH值,比较两者是否相等:如果HASH值不同,则两者必定不匹配,如果相同,由于哈希冲突存在,也需要按照BF算法再次判定。
按照此例子,首先计算子串“DEF”HASH值为Hd,之后从原字符串中依次取长度为3的字符串“ABC”、“BCD”、“CDE”、“DEF”计算HASH值,分别为Ha、Hb、Hc、Hd,当Hd相等时,仍然要比较一次子串“DEF”和原字符串“DEF”是否一致。
时间复杂度: O(m*n)实际应用中往往较快,期望时间为O(m+n)
KMP算法
Knuth Morris Pratt 算法,是由它的三位发明者 Donald Knuth、James H. Morris、 Vaughan Pratt 的名字来命名的。KMP 算法是他们三人在 1977 年联合发表的。
字符串匹配最经典算法之一,各大教科书上的看家绝学,曾被投票选为当今世界最伟大的十大算法之一;但是晦涩难懂,并且十分难以实现
对于给定文本串 T 与模式串 p,当发现文本串 T 的某个字符与模式串 p 不匹配的时候,可以利用匹配失败后的信息,尽量减少模式串与文本串的匹配次数,避免文本串位置的回退,以达到快速匹配的目的。
时间复杂度: 稳定的O(m+n)
BM算法
Boyer Moore 算法 是由它的两位发明者 Robert S. Boyer 和 J Strother Moore 的名字来命名的。BM 算法是他们在 1977 年提出的高效字符串搜索算法。在实际应用中,比 KMP 算法要快 3~5 倍
对于给定文本串 T 与模式串 p,先对模式串 p 进行预处理。然后在匹配的过程中,当发现文本串 T 的某个字符与模式串 p 不匹配的时候,根据启发策略,能够直接尽可能地跳过一些无法匹配的情况,将模式串多向后滑动几位
BM 算法的精髓在于使用了两种不同的启发策略来计算后移位数:「坏字符规则(The Bad Character Rule)」 和 「好后缀规则(The Good Suffix Shift Rule)」
这两种启发策略的计算过程只与模式串 p 相关,而与文本串 T 无关。因此在对模式串 p 进行预处理时,可以预先生成「坏字符规则后移表」和「好后缀规则后移表」,然后在匹配的过程中,只需要比较一下两种策略下最大的后移位数进行后移即可。
同时,还需要注意一点。BM 算法在移动模式串的时候和常规匹配算法一样是从左到右进行,但是在进行比较的时候是从右到左,即基于后缀进行比较。
时间复杂度: O(m/n) 最坏也是O(m*n),但是几率比Sunday小,而且可以改良成稳定的