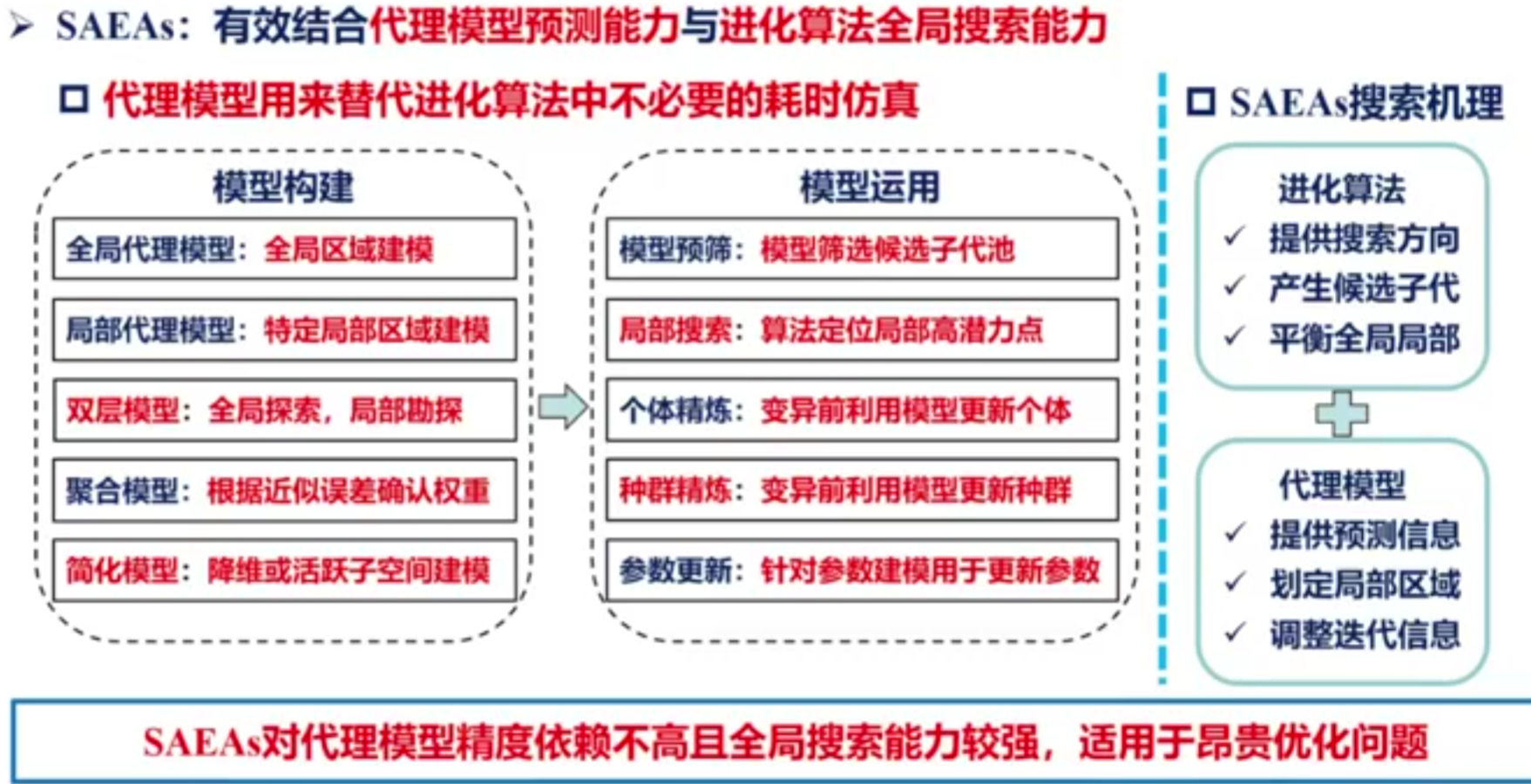
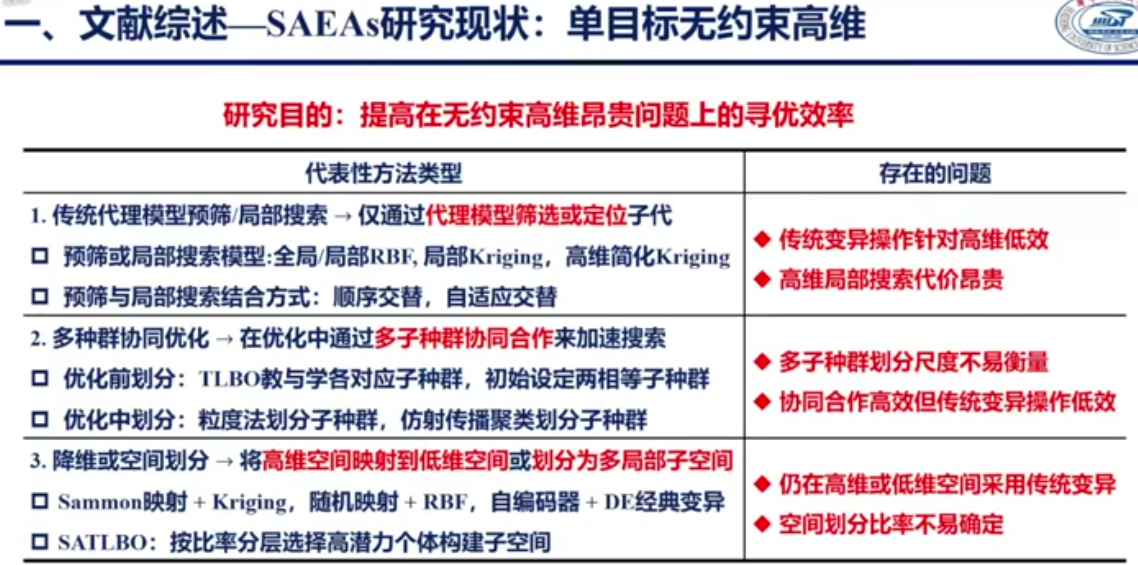
surrogate-assisted evolutionary algorithm, SAEA 也叫数据驱动的进化优化算法,因为代理模型需要真实数据去更新

使用高效的代理模型或元模型来近似进化算法(EA)中的适应度函数，是解决计算代价高昂的优化问题的有效且流行的方法

昂贵优化问题(Expensive Optimization Problem, EOP),指适应值评估昂贵(耗时)的优化问题

在许多工程优化问题中,需要昂贵(耗时)的计算或物理模拟来评估候选解决方案的质量.传统的数学优化方法不能直接用于解决这些问题,因为这些问题的分析表达式是不存在的.经典的进化算法也不适合昂贵的优化,因为它们往往需要大量的函数评估

代理模型

与标准EA相比，SAEA引入了新的步骤或问题，包括代理模型的构建、代理模型和EA之间的交互以及一些候选解决方案的重新评估。构建步骤涉及构建或更新代理模型，交互涉及将代理模型纳入EA的机制，**重新评估指的是确定一些个体(候选解)，以在优化过程中通过真实适应度函数进行评估。交互和重新评估步骤在文献中也称为模型管理(Surrogate Management)**或进化控制。

分类

代理模型分为两大类：绝对适应度模型，直接近似候选解的适应度函数值；相对适应度模型估计候选解的相对秩或偏好，而不是其适应度值。

构建

应有一个数据库(DB)存储所有的解x和真实函数评估的适应度y,表示为DB = {xi,yi}i=1N\left\{\mathbf{x}^{i}, y^{i}\right\}_{i=1}^{N} .其中N为样本数,一般要求大于变量维度D

可以通过在不使用代理模型的情况下运行几代EA或通过应用一些采样策略(也称为实验设计, DOE),例如拉丁超立方体采样(LHS)

代理模型可以根据数据库的样本点快速训练,其时间与真实函数评估的时间相比可以忽略不计.

用法

预选和估计:在个体创建中使用代理模型称为预选，在评估中使用代理模式可称为解决方案的适应度(或相对适应度)估计

模型管理

将代理模型与实际适应度函数一起使用，以防止错误收敛

模型管理的方法分为:

基于个体

在每一代中重新评估一些个体,最直观的策略是根据代理模型的适应度预测选择最适合的个体

另一方法是基于聚类技术,将种群分为几个组，然后在每个组中，重新评估离中心最近的个体

基于世代

全部个体以一个特定的频率重新评估一次

在自适应的基于世代的控制中，一个世代是否被控制(重新评估)是根据模型的保真度决定的

保真度 fidelity:能够很好地拟合真实适应度函数的模型就是高保真的

基于种群

多个子种群共同进化，每个子种群使用自己的代理进行适应性评估。允许个体从一个子群体迁移到另一个子群体

填充准则

如何从代理模型中选择合适的解来让真实函数评估在SAEA中叫填充/加点准则(infill criteria)

有如下考虑：

  1. 尽可能少的加入点，这意味着优化尽可能少的循环次数；
  2. 加入点对模型的增益最大化，这意味着我们必须充分考虑模型本身的特性，针对模型，有针对性的设计怎么加点和怎么利用加点后的数据集对模型加强训练

两个大方向:

  1. 选择最有希望的点,也就是最小点(下面的MP准则)

  2. 选择不确定性最高的点,偏探索

不确定性怎么衡量

对于一个点:

  • krg模型提供适应度(均值)估计和不确定性(方差)估计，这是适应度估计中不确定性的统计合理边界
  • 如果不是krg模型,也可以大致设置为与用于构建代理的最近数据样本的平均距离成反比
  • 基于距离的矩阵,评估现有样本点之间的距离,但在计算成本和高维空间的索引性能方面存在问题

对于一个模型:

  • 重新评估后,把误差加起来取平均
  • 个体的真实适应度与代理预测的适应度之间的均方误差

一些准则:

最小化预测 Minimizing the prediction criterion, MP

将每轮用EA得到的代理模型预测的最小点(最优点)作为加入点(即直接用代理模型的输出作为适应度)

期望改善 Expected improvement, EI

最大化当前数据最小响应点(最小y值)与我们新寻找的x点的差值(最大化“改善”)。对于每个x点，通过一些数学操作，我们可以求出这个改善的期望
具体来说，用改善的期望作为遗传算法的适应度。遗传算法得到的最优点就是加入点

概率改善 Probability of improvement, PI

最大化我们新寻找的x点的响应小于当前数据最小点的概率

同理，用概率作为遗传算法的适应度。遗传算法得到的最优点就是所加点

置信下限 Lower confidence bound, LCB

就是均值减上k倍标准差 u(x)-k*σ(x)

根据距离矩阵并行最小化预测 Parallel minimizing the prediction criterion with the distance function, DMP

Viana等人引入了一个固定距离来约束更新点。每个循环中的每个更新点的距离要大于给定值。该距离定义为0.1∗√ndim。ndim是测试问题的维数。用一个固定的距离来约束的平行最小化预测准则被称为MMP准则。以固定距离约束更新点的平行最小化预测准则被称为MMP准则。以固定距离约束更新点的平行改进概率被称为MPI准则。有固定距离约束的平行预期改进被称为MEI准则。实际更新点的影响范围与给定距离不一样。所以直接使用固定距离是不合理的。一个基于PEI的自适应距离约束被提出。该方法还使用了相关函数。

距离矩阵

DIS(x,xadd)={1R(x,xadd)<δ0R(x,xadd)>δDIS(x,x^{add})= \left\{ \begin{matrix} 1 \quad R(x,x^{add})< \delta \\ 0 \quad R(x,x^{add})>\delta \\ \end{matrix} \right.

R是相关性函数, δ是(0,1)的一个阈值

距离函数不仅避免了候选解的集中，而且提高了全局搜索能力。因为超参数是各向异性的，所以距离函数在各个方向也是各向异性的

第 q 个更新点标识为：

x(n+q)=max⁡(DMP(x,x(n+1),…,x(n+q−1)))=max⁡(MP⁡(x)∗∏i=1q−1(DIS⁡(x,x(n+q−1))))\begin{aligned} x^{(n+q)} &=\max \left(D M P\left(x, x^{(n+1)}, \ldots, x^{(n+q-1)}\right)\right) \\ &=\max \left(\operatorname{MP}(x) * \prod_{i=1}^{q-1}\left(\operatorname{DIS}\left(x, x^{(n+q-1)}\right)\right)\right) \end{aligned}

一些分类

离线/在线

离线(offline)没有增量数据(incremental data),即代理模型产生出的解不能送给真实函数评估从而反馈给代理模型

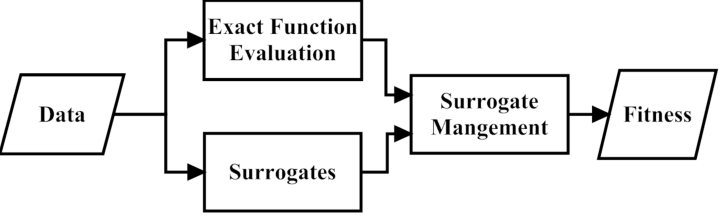
image-20220808142919538

这样会导致数据不平衡,量不够多,模型可靠性不高

一些解决手段:

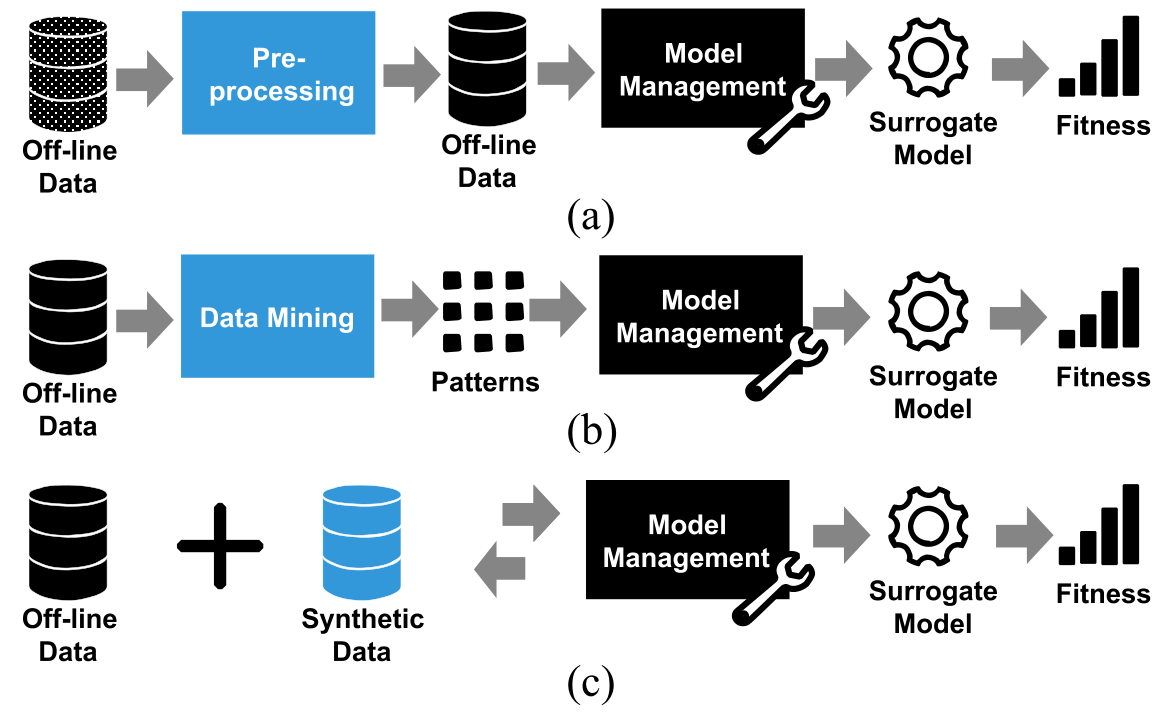
image-20221025134307737

在线(online)则可以

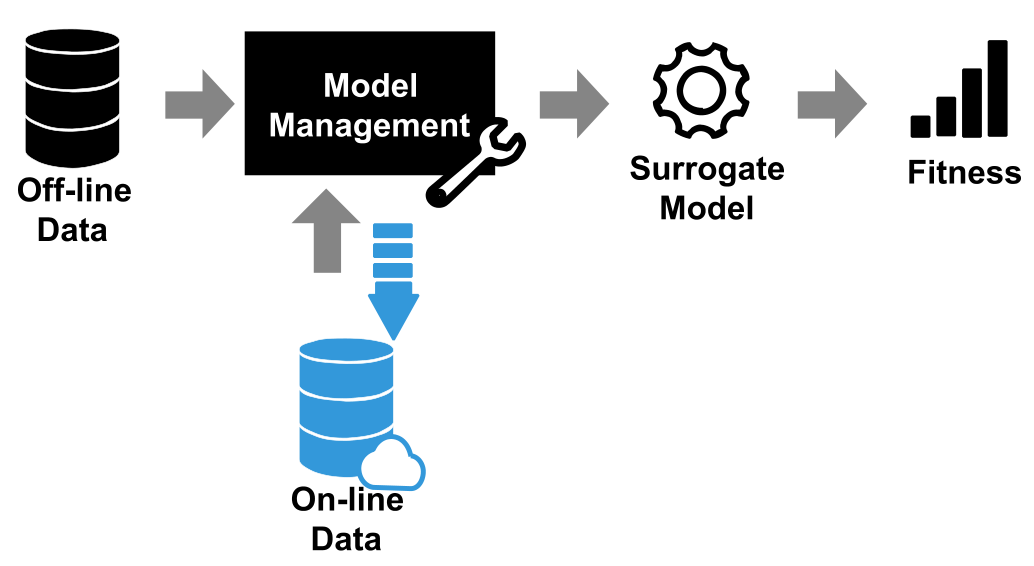
image-20221025134239089

相对适应度的代理模型

在一些实际问题中，例如适应度由人给出的交互式优化问题，解的质量很难用数值来估计，通常通过相对排序来获取。在这种情况下，只有预测候选解决方案的偏好或排名的代理模型是合适的。因此，使用代理模型来预测绝对适应值或相对适应值是选择代理模型的一个重要标准。此外，相对适应度模型定义了一种新型的替代品，可以帮助EA解决昂贵的问题。它还引入了一系列新的模型管理策略，这些策略不同于用于绝对适应度模型的策略。因此，代理模型估计绝对适应度还是相对适应度是广泛影响SAEA设计的一个重要考虑因素。

各模型简介

高斯过程(GP),Kriging(克里金)模型

常用,擅长局部,精度不错

它还能给出预测的不确定性,其他模型一般都不行

但是时间复杂度高(O(n3)左右),决策空间维数>30时很耗时

对噪声数据敏感

径向基函数 RBF

常用,比较均衡,高维问题表现不错,而且时间复杂度低,理解容易

多项式回归 PR

适合低维非线性问题中的局部建模，仅用于预测小范围内的适应度

响应面法(RSM)

很快,但只在低维(<10)时精度尚可

长期以来一直以高效率用于具有可接受的精度水平的小型问题。然而，随着问题规模的扩大，如果函数是非线性的，它就会失去效率

支持向量机 SVM

SVM 对于具有高度非线性的高维问题表现良好。近年来，SVM 也得到了发展，虽然最初的版本非常耗时，但最近的版本很快。然而，如文献中所讨论的，SVM 并不是很准确.在大多数使用 SVM 的问题中，变量的数量非常多。因此常用于高维比精度更重要的情况

此外还有人工神经网络(ANN)

套路

多代理模型/模型集合(Surrogate Ensemble)
  • 基于相同或不同的数据集建立不同的代理模型
  • 新的代理的构建将考虑现有代理所做的预测误差，可以帮劣纠正现有的代理所犯的预测错误；所有的代理组成一个组合模型，以预测计算真实的适应值
  • 每个代理模型都对最优解进行预测，然后选择预测误差较小的代理模型，从而使集成模型可以随种群进化而不断调整，提升对全局最优区域的预测准确性

多个代理模型也被用于利用 "不确定性的诅咒"和"不确定性的祝福"之间的平衡,通常借助于一个全局模型和一个局部模型.全局代理模型的目的是通过平滑掉局部优化点来捕捉适应度函数的分布情况,从而帮助优化者探索搜索空间.相比之下,局部模型是围绕当前种群发现的有希望的区域构建的,以利用适应度函数分布的局部细节.

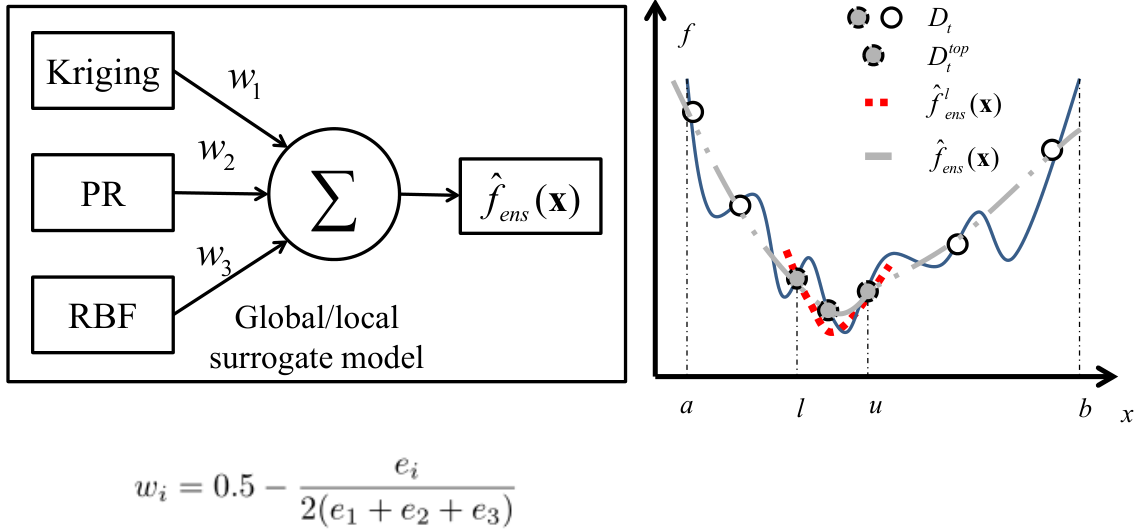
image-20220808150337696
不同的填充准则
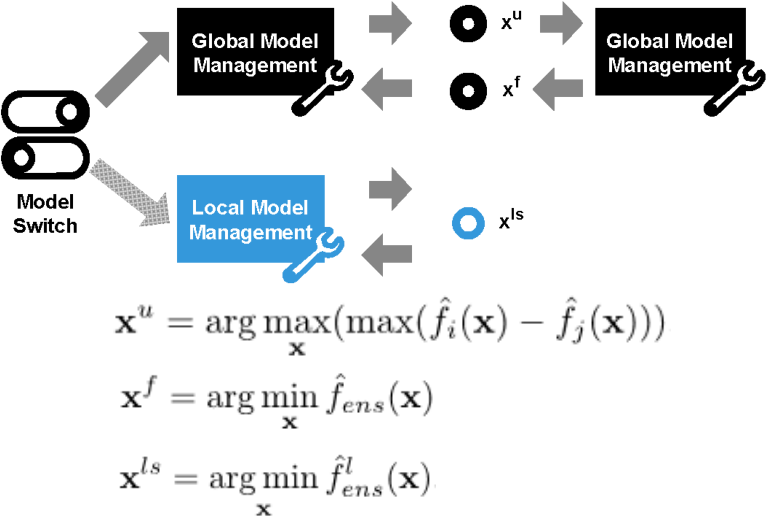
image-20220808150713785
增加代理的数据
  • 通过数据扰动，在原始数据上生成不同的数据集
  • 在现有代理有较大预测误差的地方生成数据，增加数据量
降低构造代理的计算成本
  • 在优化的早期阶段使用粗代理(保真度较低)，并随着搜索的进行逐渐提高代理的质量
基于相关性的度量,使用足够高保真度的代理
  • 使用由模型质量测量法选择的模型的SAEA的收敛性不如由保真度最高的模型辅助的SAEA好
  • 预选策略通过提高个体的质量来降低计算成本，并且可以确保优化收敛到真正的最优值。基于个体的进化控制不能保证优化过程的正确方向。因此，在大多数情况下，预选策略优于基于个体的进化控制。在某些情况下，特别是当模型足够准确以捕捉适应度函数的整体趋势时，使用基于个体的控制的 SAEA 可能比使用预选的 SAEA 表现得更好，因为前者可以比后者进化更多代。适应度函数评估是相同的。

综述

image-20220901145722858 image-20220901145933321