定义

多目标优化(MOO)

Multiobjective Optimization, 也叫MOP

在实际问题中大都具有多个目标且需要同时满足,即在同一问题模型中同时存在几个非线性目标,而这些目标函数需要同时进行优化处理,并且这些目标又往往是互相冲突的

目标函数(objective func): min⁡[f1(X⃗),f2(X⃗),…,fm(X⃗)]\min \left[f_{1}(\vec{X}), f_{2}(\vec{X}),\dots,f_{m}(\vec{X})\right]

决策向量: X⃗=[x1,x2,⋯ ,xn]\vec{X}=\left[x_{1}, x_{2}, \cdots, x_{n}\right] (里面的分量叫决策变量)

约束条件: {a≤xi≤bg(X⃗)≤ch(X⃗)=d\left\{\begin{array}{l}a \leq x_{i} \leq b \\ g(\vec{X}) \leq c \\ h(\vec{X})=d\end{array}\right. ,g(x)表示不等式约束,比如5x<6;h(x)表示等式约束,比如3x=4.

注意,多目标需要满足:

  1. 决策变量都与全部目标函数有关,不能说一部分分量只和f1有关,一部分只和f2有关
  2. 目标函数之间需要互相冲突
解的比较

支配(dominate)：如果个体i至少有一个目标比个体j好,而且个体i的所有目标都不比个体j差,那么称个体i支配个体j(xi>xj)

如果一个解决方案x∗不被任何其他可行的解所支配,则称为**帕累托最优(Pareto-optimal)**解

所有的帕累托最优解被定义为帕累托最优集(Pareto-optimal set, PS)

PS的目标向量被称为帕累托前沿 PF

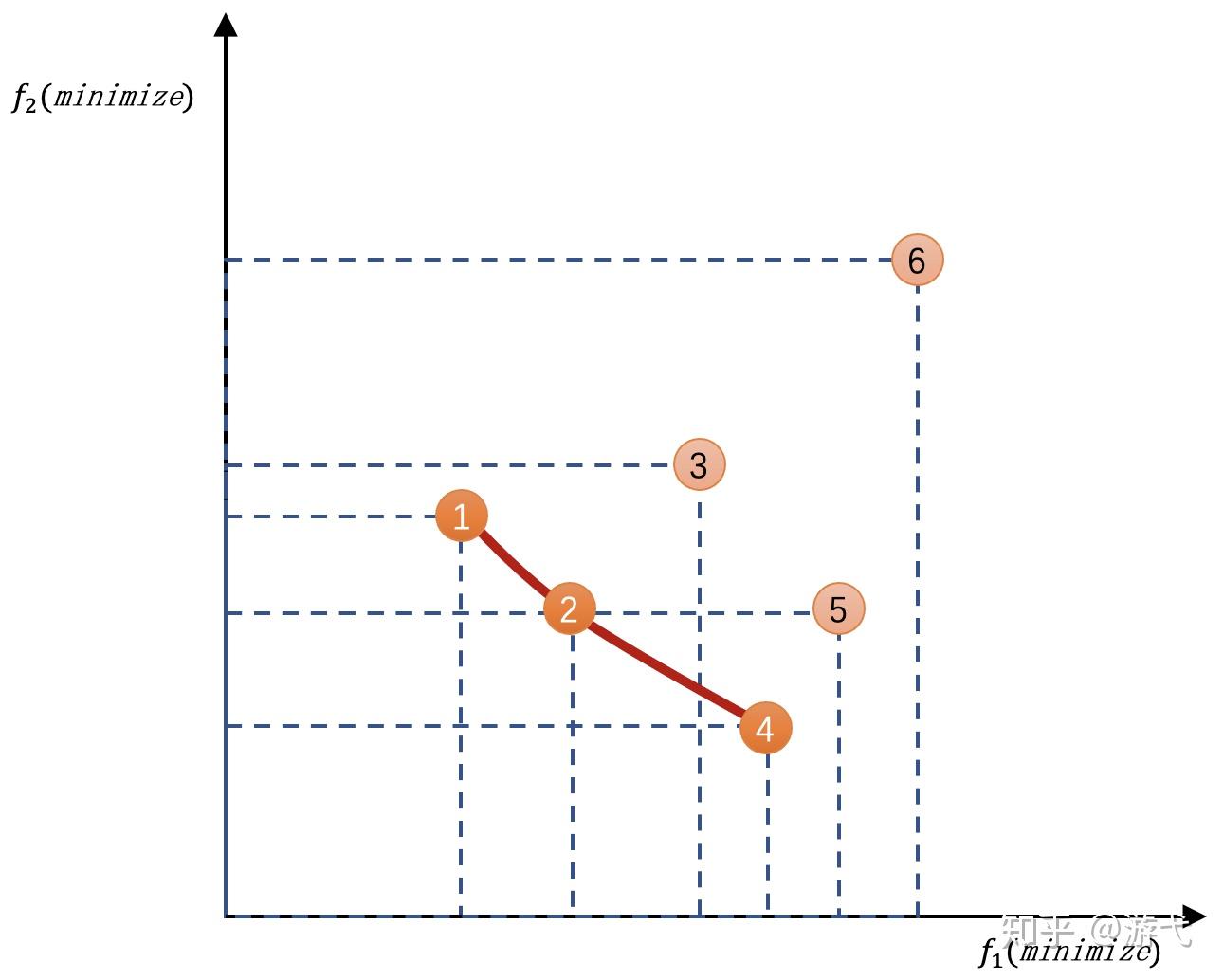
preview

假设寻找一台机器的性能,f1是时间,f2是价格,我们想要又便宜,花费时间还少的机器,图中有6台机器

2号肯定比3号好(价格时间都比3好),事实上2号右上方矩形区域的全部机器都会被2号淘汰

但是1号跟2号比就不好说,因为他们各有千秋,而且还没有被其他机器淘汰,它们就是帕累托最优解

这些帕累托最优解的机器会连成一个曲面,就是帕累托前沿

对于MOO来说,就是想找到这个帕累托前沿

在实际中,我们更关注这个曲面的3个点:最左上(图中1号)和最右下的点(图中4号),以及乌托邦点(曲面中距离图中1和4虚线交叉点最近的点,2号再靠下一点点就是)

序值
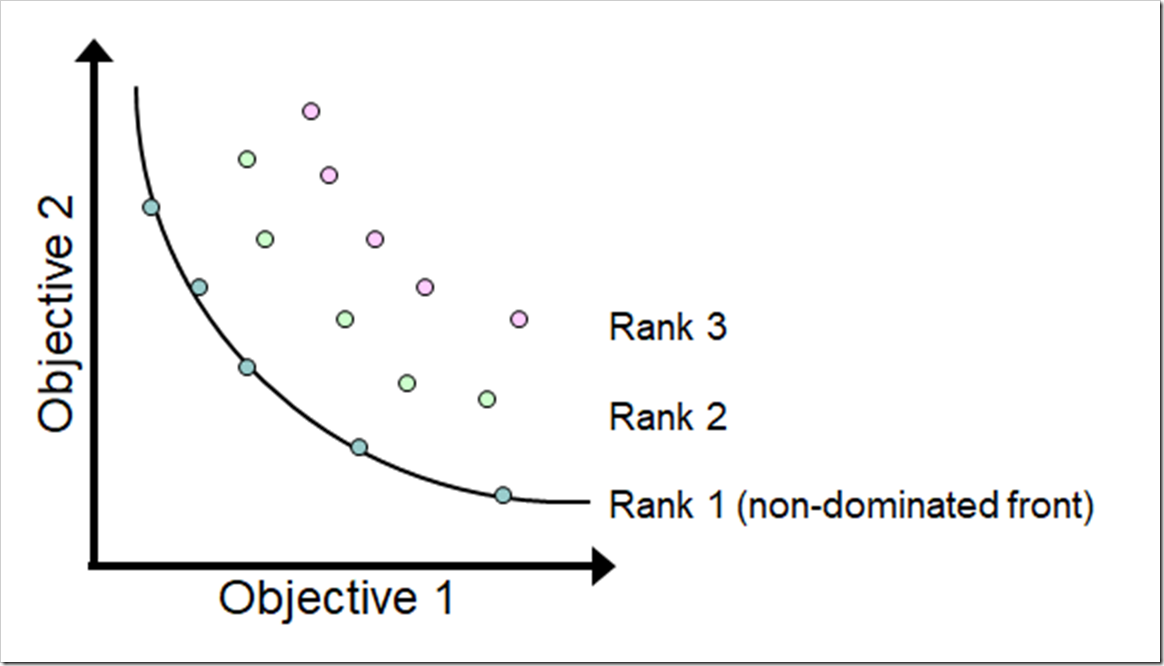
image

优化过程中不可能一下就找到真正的PF,都是从右上到左下慢慢推移的,这样可以分出多个曲面,曲面就有**序列(rank)**之分

第一序列就是PF,序值就是这个第几序列的几

如果p支配q,那么p的序值比q低.如果p和q互不支配,那么p和q有相同的序值

比如第一序列的点支配之后序列的全部点,但如果去掉第一序列的点,那第二序列的点就是最好的了(支配剩下的其他点)

拥挤距离(crowding distance)

用来计算某前沿中的某个体与该前沿中其他个体之间的距离,用以表征个体间的拥挤程度,一般把附近两个点的距离加起来就行

太拥挤不好,会导致只关注在曲面的一小部分,所以要适当调大一点距离

多任务优化(MTO)/多因子优化(MFO)

进化多任务(EMT)也叫多任务优化(Multi-task Optimization, MTO)/多因子优化(Multifactorial Optimization, MFO)

多任务优化思想就是借助任务之间隐含的并行性,对多个任务同时优化,在完成优化任务的同时提高优化效率.在MFO问题中,同时进行的多个任务的依赖性是提前不可预知的,且任务之间的搜索空间可以相同也可以不同.另外,MFO支持连续与离散的任务同时处理.

一个比较极端的例子:

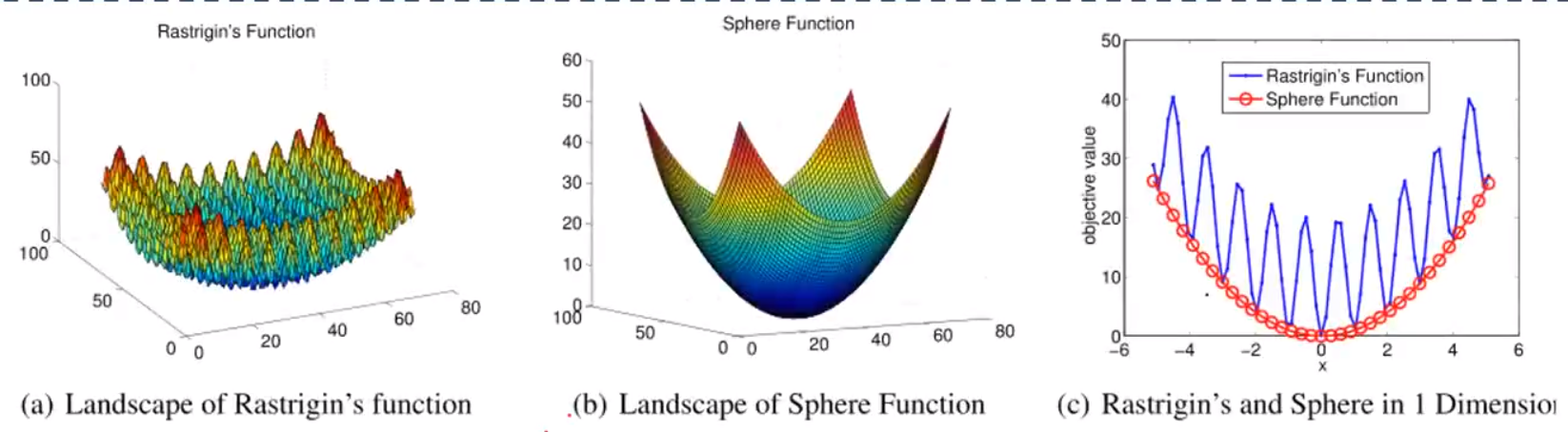
image-20220626153304820

a图很难求解,但b图容易,一维下ab的好的解比较像,所以b可以辅助a

MTO要优化的东西叫任务,我们定义一个任务T为:

{minf(x)s.t.ga(x)≤0,a=1,2,...,qhb(x)=0,b=1,2,...,p\begin{cases} min & f(x)\\ s.t. & g_a(x) \leq 0,& a=1,2,...,q\\ & h_b(x) = 0,&b=1,2,...,p \end{cases}

它具有a个不等式约束条件与b个等式约束条件的最小值优化.ga(x)表示第a个不等式约束,hb(x)表示第b个等式约束

假设待优化的各个任务之间相互独立,即不给出任何各个任务之间的依赖关系的先验知识.同时,假设所有任务都是求最小值(求最大值的可以转换为求最小值),即每个任务都是一个连续单目标最小化问题

那一个MTO问题可以定义为:

xi∗=arg⁡min⁡Fi(x),i=1,2,…,K\mathbf{x}_{i}^{*}={\arg \min } F_{i}(\mathbf{x}), i=1,2, \ldots, K

Fi为要解决的第i个任务的目标函数,K是任务数

多任务优化问题就是同时找到K个全局最优解{x∗1,x∗2,...,x∗k},分别使对应的目标函数Fi最小

与单任务优化不同,MTO需要新的个体适应度和比较标准,因此MTO中的每个个体i都有以下新属性:

  1. factorial cost 因子成本: 个体i在任务j上的因子成本: Ψji=λ⋅δji+fji\Psi_{j}^{i}=\lambda \cdot \delta_{j}^{i}+f_{j}^{i}, 其中λ是一个大的惩罚系数,δij是i对于j约束条件违反情况,fij就是j的目标函数值.

    最常见的:如果i相对于j来说是可行的(零约束违反),就有Ψji=fji\Psi_{j}^{i}=f_{j}^{i},这时候就是任务的目标函数值(也是传统EA的适应度)

    PS.因子成本一般是越小越好.因为是多任务,所以一般是向量形式

  2. factorial rank 因子排名: 个体i在任务j上依据因子成本的排名,比如j上最佳个体i,它的因子排名 rij=1r_{i}^{j} = 1

    PS.因为是多任务,所以一般是向量形式

  3. skill factor 技能因子: 个体i的技能因子是它最拿手任务的索引.给定个体i在所有任务上的因子排名rijr_{i}^{j} ,其技能因子就是排名最靠前(值最小)的那个任务的索引 τi=argmin⁡jrij\tau_{i}=\operatorname{argmin}_{j} r_{i}^{j}

    要是有排名相同的就随便选其中一个任务作为绝活

    比如一个个体在4个任务的因子排名分别是2,4,3,6.则该个体的技能因子是1,也就是说该个体在1号任务上表现最好

  4. scalar fitness 标量适应度: 把所有个体的适应度值统一标量化,个体间就可以直接进行性能对比了.取所有任务中因子排名的最小值进行倒数 φi=1/min⁡j∈{1,…,K}{rji}\varphi_{i}=1 / \min _{j \in\{1, \ldots, K\}}\left\{r_{j}^{i}\right\}

    比如一个个体在4个任务的因子排名分别是2,4,3,6.则该个体的标量适应度就是1/2,然后看它的技能因子就知道是1号任务绝活

    如果任务pa的标量适应度大于pb,就认为pb在多因素意义上支配(dominate)了pb(pa>>pb)

因子成本直接计算任务的目标函数值,因子排名需要根据因子成本排序获得,技能因子需要因子排名的最小值索引,标量适应度需要因子排名的最小值

当两个个体的factorial rank相同时,同时将这两个个体称为j-counterparts(j对应关系)

当两个个体的factorial rank与skill factor均相同时,称之为strong counterparts(强对应关系)

对于个体p*,如果它在所有任务表现均为最优时,就称之为多因素最优(multifactorial optimality)

MOO与MFO/MTO的区别

  1. MOO中的函数/任务是在同一个决策空间中定义的,而MTO中的函数/任务可以有不同的决策空间.
image-20220626154044059
  1. MOO试图在不同目标之间找到一个良好的权衡,即在PF上找到一组有代表性的解.但帕累托最优的概念在MTO的规定范围内是不存在的,MTO的目的是利用任务间的知识转移,找到至少一个优化任务的全局最优(一个解找到一个最优就算成功)
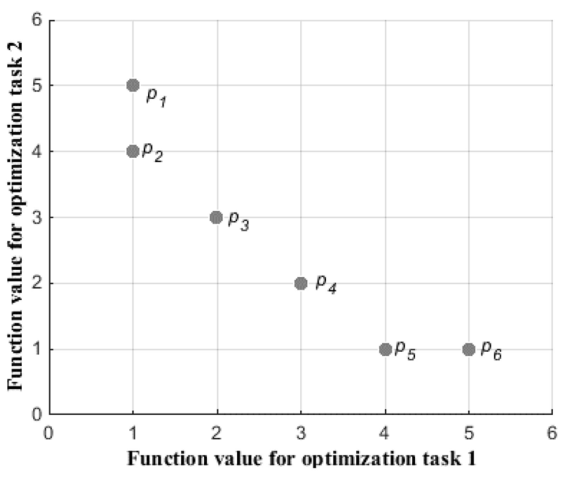
image-20220517175223234

上图中描述了一个双任务问题的目标空间.从非支配性原则来看,个体{p2, p3, p4, p5}属于第一非支配性前沿,而{p1, p6}则属于第二非支配性前沿.换句话说,个体{p2, p3, p4, p5}之间没有孰优孰劣,而且他们总是比{p1, p6}好.

然而,根据MTO的定义,个体p1和p2(还有p5和p6)被标记为强对应关系(p1和p2对于任务1的函数值都是1,而且都是解决任务1的第一名).此外,{p1, p2, p5, p6} >> {p3, p4}.换句话说,{p1, p2, p5, p6}之间在多因素意义上被认为是没有孰优孰劣的,并且总是比{p3, p4}好.因为p5和p6在任务1上表现很好,p1和p2在任务1上表现很好,我们不关心它们在其他任务上的表现如何.

多因子进化算法(MFEA)

multifactorial evolutionary algorithm

MTO是基于EA框架的,在此基础上同时解决多个优化任务,通过任务间的知识转移提高独立解决每个任务的性能

MFEA是最广泛使用的EMT算法之一,算法保留了传统EAs算法的种群初始化、评价、后代生成和环境选择等一般流程,但是多了一些环节.

基本流程

输入:种群大小NP,任务数K. 输出:全部任务的最好的解 image-20220714142343340

  1. 随机生成一个初始种群(方法见编码方式),把它存到当前种群P中
  2. 将P中全部个体按任务号顺序分配技能因子(保证每个任务被个体关联的个数平均)(原始论文的做法不同,全分配0并对所有任务评估)
  3. 分配完后对个体评估(解码,计算因子成本,因子排名),不用对所有任务评估
  4. 当不满足终止条件(一般是进化代数或者提升不多)时:
  5. 根据算法2(同种交配),从P中生成后代种群O
  6. 根据算法3(垂直文化传播),O的个体获得其父母的技能因子
  7. 评估O的个体
  8. 把P和O拼接成一个大的中间种群R
  9. 更新R的标量适应度
  10. 根据选择算子(精英策略,需要根据标量适应度排序)从中间种群中选出下一代种群P

编码方式

和传统EA/GA不同,MFEA使用了不同的编码方式:统一搜索空间(unified search space),也叫隐式EMT

对于多个优化任务,它们各自的维数Dj都不同.统一搜索空间Y的维数设为所有任务中最高维数max{Dj}=Dmultitask

每个个体都用Dmultitask维的向量yi表示,在处理任务Tj时,我们只需去看染色体的前Dj个分量(也叫键,key).

在种群初始化步骤中,每个个体初始化一个Dmultitask维的随机向量yi(里面的值随机,取值范围[0,1],与问题解的范围无关)

比如有两个任务,一个10维(10个变量),一个20维.那每个个体都要弄成20维的向量,但处理第一个任务时只需要前10个分量就可以(arr[:10])

PS.个体的向量的值是浮点数,即使基础问题是离散的.离散问题根据问题的不同,编码方式也有不同

使用这种编码技术,而不是和传统GA一样,简单地将每个优化任务的决策变量连接起来,形成一个由D1+D2+...+DK个元素组成的巨大染色体,其动机有两个方面:

  1. 当需要同时解决几个具有多维搜索空间的任务时,这样有助于规避与维度诅咒有关的挑战.
  2. 方便知识在不同的任务之间共享

不过用统一搜索空间编码的话,解码就没那么容易了

PS. 实现任务间知识转移的典型转移方案有三种:统一表示方案(如上)、随机对齐方案和显式自动编码

解码/编码

个体i的决策变量xi在优化/搜索之前需要先编码变成zi,以便知识迁移.优化完成之后解码变回xi,以便用真实函数评估或计算个体的因子成本

对于连续优化的情况下:考虑实际问题的第i个决策向量(xi)的解在[Li, Ui]的范围内,编码后对应的值为zi

那么它在实际问题的搜索空间中的映射(解码)就是 xi = Li + (Ui - Li) * zi

对应的编码就是 zi = (xi - Li) / (Ui - Li)

对于离散优化的情况,染色体解码方案通常取决于问题

选择算子

MFEA遵循一种精英策略,确保最佳个体能够世代生存.根据标量适应度排序后选择靠前的个体组成新的种群

遗传/生成后代机制

传统EA采用交叉和变异算子,MFEA也差不多,但是两个随机选择的候选父母必须满足某些条件才能进行交叉,即同种交配(assortative mating),就是个体更愿意与相同文化背景(cultural background)的人交配.

技能因子τ就是个体文化背景的数值表示.因此如果两个随机选择的候选父母拥有相同的技能因子,就可以自由地进行交叉.或者如果他们的技能因子不同,则按照规定的**随机交配概率(rmp)**进行交叉.还不行就会选择突变.算法2就是根据上述规则创造后代(offspring)的步骤.

输入:两个随机选择的父代个体p1,p2;两个父母的技能因子τ1,τ2;随机交配概率rmp image-20220714145343174

输出:两个后代个体o1,o2

  1. 如果两个父母的技能因子一样 或者 随机概率<rmp:

  2. 父母通过交叉生成后代

  3. 否则:

  4. o1通过p1变异生成

  5. o2通过p2变异生成

上述过程中使用的是两种较为流行的遗传算子:模拟二进制交叉(Simulated Binary Crossover, SBX)和多项式变异(polynomial mutation)

参数rmp被用来平衡搜索空间的利用和探索.rmp值接近0意味着只允许文化相近的个体进行交配,而接近1的值则允许完全随机交配.在前一种情况下,主要发生的是的文化内交配(即具有相同技能因素的父母候选人之间)和突变产生的小的变异(当父母候选人具有不同的技能因素时发生),这有利于扫描搜索空间的有限区域.但解决方案总是有陷入局部优化的趋势.相反,在rmp值较大(接近1)的情况下,跨文化交配的增加使得对整个搜索空间的探索得到加强,从而有利于摆脱局部最优状态.此外,属于同一文化背景的个体之间的排他性交配可能会导致其他文化背景的良好和多样化的遗传材料的损失.因此,必须适当选择rmp,以确保在彻底扫描搜索空间内的较小区域和探索整个空间之间取得良好的平衡.

模拟二进制交叉 SBX

c1(t)=0.5[(1+γ)p1(t)+(1−γ)p2(t)]c2(t)=0.5[(1−γ)p1(t)+(1+γ)p2(t)]\begin{aligned} &\mathbf{c}_{1}(t)=0.5\left[(1+\gamma) \mathbf{p}_{1}(t)+(1-\gamma) \mathbf{p}_{2}(t)\right] \\ &\mathbf{c}_{2}(t)=0.5\left[(1-\gamma) \mathbf{p}_{1}(t)+(1+\gamma) \mathbf{p}_{2}(t)\right] \end{aligned}

γ={(2u)1η+1, if 0<u≤0.5(12−2u)1η+1, if 0.5<u<1\gamma= \begin{cases}(2 u)^{\frac{1}{\eta+1}}, & \text { if } 0<u \leq 0.5 \\ \left(\frac{1}{2-2 u}\right)^{\frac{1}{\eta+1}}, & \text { if } 0.5<u<1\end{cases}

其中p1(t)和p2(t)是第t代的亲代个体;c1(t)和c2(t)是第t代产生的子代个体;η是分布指数,η>0;u是0到1之间的随机数

程序中我们只需给定η的值就可以了,η的变量名一般叫mu

多项式变异 PM

c(t)=p(t)+βp(t)\mathbf{c}(t)=\mathbf{p}(t)+\beta \mathbf{p}(t)

β={(2u)1η+1−1, if 0<u≤0.51−[2(1−u)]1η+1, if 0.5<u<1\beta=\left\{\begin{array}{l} (2 u)^{\frac{1}{\eta+1}}-1, \quad \text { if } 0<u \leq 0.5 \\ 1-[2(1-u)]^{\frac{1}{\eta+1}}, \quad \text { if } 0.5<u<1 \end{array}\right.

其中,p(t)是亲代个体,c(t)是第t代中通过变异p(t)产生的子代个体;η是分布指数,η>0;u是一个0到1之间的随机数.

程序中我们只需给定η的值就可以了,η的变量名一般叫mum

后代评估机制

为每一个任务评估每一个个体往往在计算上过于昂贵,因此是不可取的.为了使MFO在计算上实用,MFEA必须被设计成高效的.这一点在这里是通过尽可能多地减少函数评价的总数来实现的.我们所做的一个重要观察是,在MFEA中生成的个体不太可能在所有的任务中都表现出色.因此,一个个体最好只对它最有可能表现良好的任务进行评估

垂直文化传播(vertical cultural transmission)是一种遗传模式,其现象是后代的表型直接受到其父母表型的影响.该现象搬到MFEA中就是后代模仿(获得)其父母之中一个个体的技能因子(文化背景),技能因子体现了个体表现最好的任务,所以就只对这个任务进行评估.这一方法被称为选择性模仿(selective imitation).如果后代只有一个父母,就直接模仿该父母的技能因子,只评估对应的任务

输入:后代个体o,还有它父母的信息(起码得知道技能因子)image-20220714150611200

输出:o要模仿的技能因子

  1. 如果o有两个父母p1,p2:
  2. 如果概率<0.5:模仿p1的技能因子
  3. 不然:模仿p2的技能因子
  4. 否则就是只有一个父母:那就直接模仿它的技能因子

原始论文中,其他任务的因子成本设成无限.不过反正只对技能因子对应的任务评估,其他任务的值是多少都无所谓的

算法总结

MFEA根据技能因子的不同将种群分为不同的技能组.然而,不同组的遗传物质也有可能对另一组产生作用.通过设置好的rmp概率与子代对父母技能的模仿实现不同技能组之间的通信,从而使遗传物质在不同技能组之间转移.相互沟通的遗传物质是实现算法隐含并行性的关键原因

杂项

多任务带来了什么好处?

  1. 在存在遗传互补性的情况下,从简单任务到复杂任务的隐式遗传转移可以导致复杂优化任务的快速收敛
  2. 两个复杂任务之间的遗传交换有助于同时利用两个函数概览,从而有效地避开障碍以更快地收敛

常用的测试函数

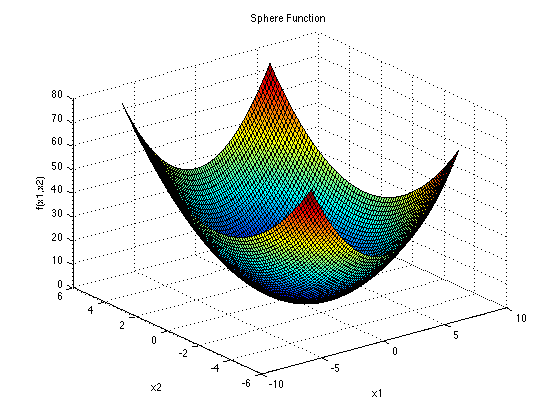
SPHERE:f(x)=∑i=1dxi2f(\mathbf{x})=\sum_{i=1}^{d} x_{i}^{2}

Sphere函数有唯一一个全局最小值,它是一个简单的单模态函数,无需知识转移就能快速解决.

img

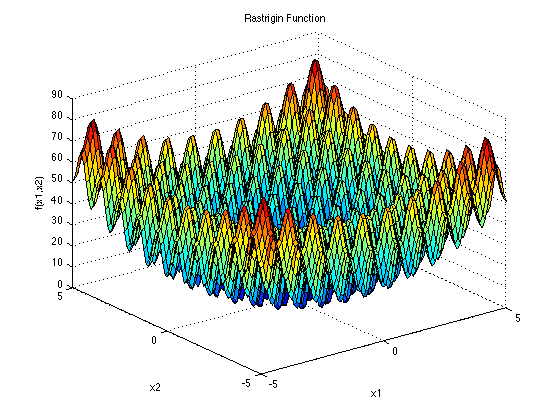
RASTRIGIN:f(x)=10d+∑i=1d[xi2−10cos⁡(2πxi)]f(\mathbf{x})=10 d+\sum_{i=1}^{d}\left[x_{i}^{2}-10 \cos \left(2 \pi x_{i}\right)\right]

Rastrigin函数是一个相对复杂的多模态函数,包含大量的局部最优值.它与Sphere函数类似,两个函数都有相同的全局最小值.因此,Sphere可以成为Rastrigin的一个很好的辅助任务.

img

ACKLEY:f(x)=−aexp⁡(−b1d∑i=1dxi2)−exp⁡(1d∑i=1dcos⁡(cxi))+a+exp⁡(1)f(\mathbf{x})=-a \exp \left(-b \sqrt{\frac{1}{d} \sum_{i=1}^{d} x_{i}^{2}}\right)-\exp \left(\frac{1}{d} \sum_{i=1}^{d} \cos \left(c x_{i}\right)\right)+a+\exp (1)

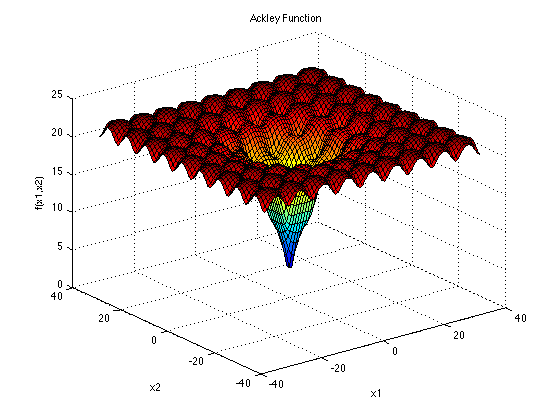
Ackley是一个更简单的多模态函数,用来检测一个算法的全局收敛速度.维度增加的时候,它的方向梯度前进的方向是各种各样的

img

衍生形式

MEFA的优缺点

优点:在积极的任务间知识迁移的帮助下,能有效地加速收敛和增强全局搜索能力.

缺点:

  1. 现有的多任务EA主要集中在解决少数几个任务(如两个任务),并且它们假设要解决的任务之间存在相似性.当有多个任务需要解决,且任务之间的相似性事先未知时,现有的多任务EA就很难有效地解决这些任务.主要的困难在于定义一个有效的知识转移策略.如果该假设不成立,任务之间可能会发生负转移,这可能会导致MFEA的性能比完全没有转移的相应的单任务EA更差.即知识迁移的质量很影响最后结果
  2. 在进化算法能够找到一个可接受的解决方案之前,通常需要进行大量的适应度评价,这严重阻碍了EA的应用,使其无法应用于现实世界中的优化问题,因为一次适应度评价可能需要几分钟到几个小时
自动生成辅助任务

辅助任务可以帮助EA获得更好/更快结果

目前有两种方法:

  1. 多目标化,解决知识迁移的质量问题
  2. surrogate模型(代理模型),它是一个近似模型,解决适应度评价费时问题

广义多因子进化算法(G-MFEA)

Generalized MFEA

MFEA的缺陷

传统MFEA中统一搜索空间有缺陷:

  1. MFEA中的统一搜索空间的取值范围是[0,1],而不同问题最优点的位置不同,这样很容易发生负迁移

  2. 如果MFO问题中不同任务的决策空间的维度不同,MFEA中的知识转移效率可能会降低.

不同问题最优点的位置不同

同种交配是MFEA的一个重要特征,它能够通过允许不同任务的个体交配来促进种群多样性.

对于一个MFO问题,如果其最优点都位于统一搜索空间Y的同一位置:

在优化过程中,与不同任务相关的个体很可能分布在不同的位置,而到优化结束时,它们会收敛到同一位置.因此,每个任务的个体在优化过程的早期阶段能够保持高度的多样性,这种多样性随着进化的进行而减少,这有利于提高优化过程后期的收敛性.

然而,如果MFO问题的最优点位于不同的位置,即使在优化过程的后期,每个任务的个体仍然是相互远离的.

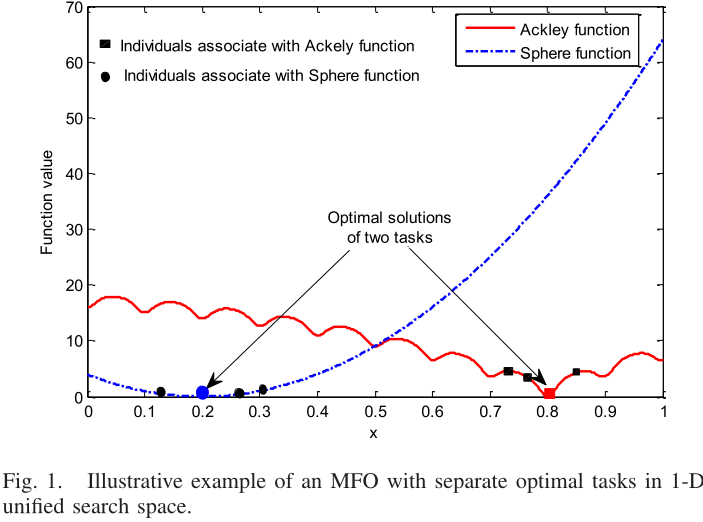
image-20220713142747822

图1显示了一个在一维统一搜索空间Y中具有不同最优点的MFO问题的例子.根据上面的分析,在整个优化过程中,同种交配将为种群引入多样性.然而,由于最优点位置不同,过度的多样性可能会严重减慢搜索任务最优解的收敛速度

不同任务的决策空间的维度不同

垂直文化传播是MFEA的另一个关键特征,它在不同的任务之间交换解决方案.它的目的是将高质量的解决方案从简单任务转移到复杂任务.然而如果不同任务决策空间的维度不同,效果就不好

image-20220713143215669

如图2所示的示例,其中MFO问题包含两个任务,即task1和task2,其维度分别为7和10.在这种情况下,task1中的个体只有第一部分(前7个决策变量)代表解决方案,而其余变量不使用.因此,task2的最后几个变量无法与task1交换知识.此外,任务1的好方案不一定对任务2好,因为它对任务2来说是一个非整合的方案.因此,当任务1和任务2的维度不一致时,MFEAs中知识转移的有效性可能会降低

两个策略

G-MFEA采用了两种新的策略:**决策变量翻译策略(decision variable translation strategy)**解决第一个缺陷;**决策变量洗牌策略(decision variable shuffling strategy)**解决第二个缺陷

决策变量翻译策略将个体的解映射到一个新的空间,其中所有任务的最优解都位于同一位置,可以在增强种群多样性和加速种群收敛之间保持更好的平衡

决策变量洗牌策略首先随机改变低维度解决方案中的变量顺序,使每个变量有机会在两个任务之间进行知识转移.然后,低维任务的个体没有使用的决策变量被高维任务的个体的决策变量所取代.

决策变量翻译策略

决策变量转换策略要求所有最优值都转移到统一搜索空间的中心点,即cp=(0.5,0.5,...,0.5).为了实现这一点,重要的是估计从每个任务的当前位置到中心点的距离,称为翻译方向 dk=sf×α(cp−mk),k=1,2,…,K(4)d_{k}=\mathrm{sf} \times \alpha\left(\mathrm{cp}-m_{k}\right), k=1,2, \ldots, K \\ (4) .它是一个向量,维数=任务维数,共K个,K是任务数(说明与个体无关)

其中mk是通过计算第k个任务的前μ%最佳解的平均值.由于估计的最优解mk可能与真实的最优解不同,可能小于真实的翻译方向.这可能导致任务不能被翻译到同一空间的情况,甚至直到进化优化的最后都不行.为了确保在优化过程中,两个任务的位置能够在一定时间内重叠,我们在每一步使用比例系数sf稍微加快了翻译距离

为了保持稳定的平移,每一个θ代计算dk,如算法5中的步骤2-4.考虑到早期优化过程中对最优值的估计不准确,α被初始化为零,并随着第φ代的进化而逐渐增加:α=( gen  Maxgen )2\alpha=\left(\frac{\text { gen }}{\text { Maxgen }}\right)^{2}

一旦估计出翻译方向,每个个体就会根据以下公式移动到一个新的位置:pˉi=pi+dτi(6)\bar{p}_{i}=p_{i}+d_{\tau_{i}} \\ (6) τi是第i个个体的技能因子,意思就是根据该个体的绝活任务来加减一下各决策变量

输入:当前进化代数gen,最大进化代数Maxgen,当前种群P,种群大小NP,改变翻译方向的频率θ,启动决策变量翻译策略的阈值Φ

输出:翻译后的种群Pˉ\bar P image-20220713144117146

  1. 如果进化代数gen>阈值Φ:

  2. 因为每个任务的翻译方向每θ代更新一次,如果mod(gen,θ)=0,就说明到更新的时候了

  3. 根据(4)计算每个任务的翻译方向

  4. end if

对当前种群的每个个体,根据(6)计算翻译后的个体pˉi\bar{p}_{i}

  1. 并把它加到Pˉ\bar P里

  2. end for

  3. 不然的话:

  4. Pˉ\bar P就是P,原封不动

实际实现中mk也要洗牌,以做到dk维数统一

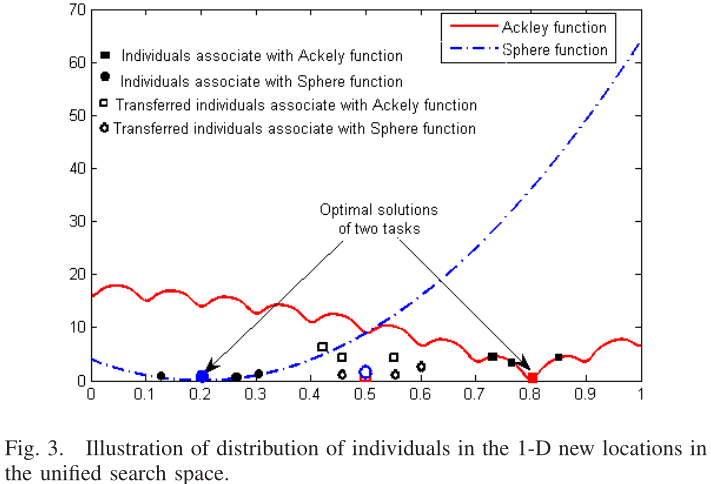
图1的翻译结果如图3:

image-20220713153428304

决策变量洗牌策略

决策变量洗牌策略首先随机改变低维度解决方案中的变量顺序,使每个变量有机会在两个任务之间进行知识转移.然后,低维任务的个体没有使用的决策变量被高维任务的个体的决策变量所取代.由于这个原因,决策变量洗牌策略只能应用于具有较低维度的父母.

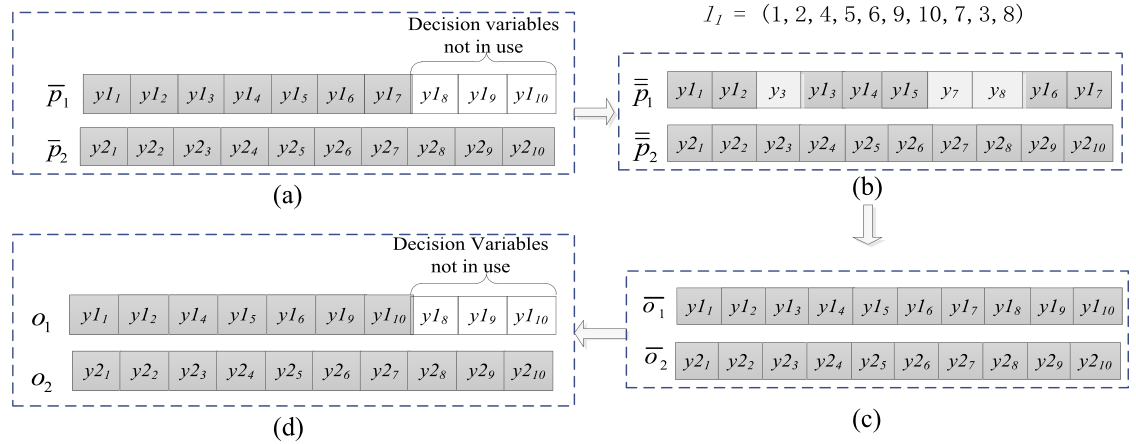
image-20220713161838622

上图展示了一个例子来说明决策变量洗牌策略的主要思想,两个父代pˉ1和pˉ2\bar p_{1}和\bar p_{2}是从Pˉ\bar P中随机选择的,分别与任务1和任务2相关.假设任务1的维度低于任务2,因此,只有P1会受到决策变量洗牌策略的影响.

我们首先记录这两个人的决策变量的顺序为l1 = 1,2,...,Dmax; l2 = 1,2,...,Dmax.其中Dmax = max(D1, D2)

然后从Pˉ\bar P中随机选择一个与任务2(pˉ2\bar p_{2}关联的任务)相关的额外个体pˉ\bar p =(y1, y2, ..., y10),用来替换p1中未使用的变量

之后,通过合并pˉ\bar p和pˉ1\bar p_{1},将得到交替的pˉˉ1\bar{\bar{p}}_{1}.做法:列表l1被随机打乱,索引在列表l1前D1维元素中的变量来自pˉ1\bar p_{1},而其余变量来自pˉ\bar p.

如图(b):原先的3,7,8号位被额外个体的y3,y7,y8所替代

一旦决策变量洗牌完成,初始子代oˉˉ1和oˉˉ2\bar{\bar{o}}_{1}和\bar{\bar{o}}_{2}将由pˉˉ1和pˉˉ2\bar{\bar{p}}_{1}和\bar{\bar{p}}_{2}通过同种交配产生,这些子代必须被翻译回原始解空间.图(c)是已经从初始子代翻译回原空间的子代oˉ1和oˉ2\bar o_{1}和\bar o_{2}(算法4的第8步,这步跟洗牌无关,只是为了说明下面的恢复操作)

如果一个子代洗过牌,那真正放到子代种群前,决策变量的顺序需要重新改变,简单来说就是把之前被替代的变量删掉,空出位置恢复成原来任务的维数.图(d)是一个例子,由o1(1:D1)=o‾1(l1(1:D1))o_{1}(1:D_{1})= \overline{o}_{1}(l_{1}(1:D_{1}))得到的o1作为任务1的子代,而oˉ2\bar o_{2}本身就是任务2的子代o2

输入:从已翻译种群Pˉ\bar P中随机选择的两个父代个体pˉ1和pˉ2\bar p_{1}和\bar p_{2} image-20220721141551309

输出:两个洗牌后的父代个体pˉˉ1和pˉˉ2\bar{\bar{p}}_{1}和\bar{\bar{p}}_{2},以及对应的决策变量的顺序记录l1和l2

设:Dmax是任务维数较高的那个,l1和l2初始化为[1,2,...,Dmax]

  1. 获取pˉ1和pˉ2\bar p_{1}和\bar p_{2}的技能因子τ1,τ2

  2. 如果是D1维数更小(pˉ1\bar p_{1}要洗牌):

  3. 从Pˉ\bar P随便选一个技能因子=τ2的个体pˉ\bar p

  4. 打乱l1

  5. 索引在列表l1前D1维元素中的变量来自pˉ1\bar p_{1},而其余变量来自pˉ\bar p

  6. pˉ\bar p和pˉ2\bar p_{2}作为pˉˉ1和pˉˉ2\bar{\bar{p}}_{1}和\bar{\bar{p}}_{2}输出

  7. 否则就是D1维数更小(pˉ2\bar p_{2}要洗牌):

  8. 8-11和第一种情况类似

  9. 不然就是两个任务维数一样

  10. 那就什么都不做,直接输出pˉ1和pˉ2\bar p_{1}和\bar p_{2}

算法流程

G-MFEA与MFEA的不同之处主要在于子代的产生过程.在每一代中,原始种群中个体的位置首先通过决策变量翻译策略转换到一个新的位置,新位置的种群用Pˉ\bar P表示,算法5详细说明了决策变量转换策略.一旦翻译后的种群Pˉ\bar P形成,将从Pˉ\bar P中的父母中产生后代.给定两个随机选择的父母,决策变量的顺序被进一步扰乱,在他们进行同种交配之前,不使用的变量被决策变量洗牌策略取代.决策变量洗牌策略在算法6中描述.

输入:种群大小NP,任务数K. 输出:每个任务的最好的解

超参数: θ:改变翻译方向的频率,每个任务的翻译方向每θ代更新一次.Φ:启动决策变量翻译策略的阈值

  1. 初始化种群P,分配技能因子以及评估(和MFEA一样) image-20220713144250403
  2. 当不满足终止条件时:
  3. 通过决策变量翻译策略从P中生成Pˉ\bar P
  4. For:把Pˉ\bar P分成两半
  5. 左半和右半各随机选一个个体作为父代,记为pˉ1和pˉ2\bar p_{1}和\bar p_{2},获取它们的技能因子
  6. 通过决策变量洗牌策略从pˉ1和pˉ2\bar p_{1}和\bar p_{2}生成pˉˉ1和pˉˉ2\bar{\bar{p}}_{1}和\bar{\bar{p}}_{2}
  7. 通过同种交配(SBX和PM)从pˉˉ1和pˉˉ2\bar{\bar{p}}_{1}和\bar{\bar{p}}_{2}生成子代 oˉˉ1和oˉˉ2\bar{\bar{o}}_{1}和\bar{\bar{o}}_{2}
  8. 从子代oˉˉ1和oˉˉ2\bar{\bar{o}}_{1}和\bar{\bar{o}}_{2}翻译回原始解空间生成oˉ1和oˉ2\bar o_{1}和\bar o_{2}
  9. 垂直文化传播,子代oˉ1和oˉ2\bar o_{1}和\bar o_{2}获得父代的技能因子
  10. 因为子代oˉ1和oˉ2\bar o_{1}和\bar o_{2}可能洗过牌,所以要恢复决策变量的位置顺序,生成o1和o2o_{1}和o_{2},加入后代种群O中
  11. end for
  12. 评估后代种群O
  13. O和P拼接生成R
  14. 更新R的标量适应度
  15. 根据选择策略(精英策略)选择NP个个体形成新种群P

应该注意的是,生成的子代也在翻译后的解空间中.因此,这些子代必须被翻译回原始解空间(步骤8).一个子代被翻译回与它有更紧密继承关系的父代的空间(看技能因子),比如:oˉ1=oˉˉ1−dτ1.\bar{o}_{1}= \bar{\bar{o}}_{1}-d_{\tau _{1}}.

在利用垂直文化传播为子代分配技能因子后,每个子代的决策变量恢复决策变量的位置顺序(步骤10)

NSGA-II 多目标进化算法(MOEA)

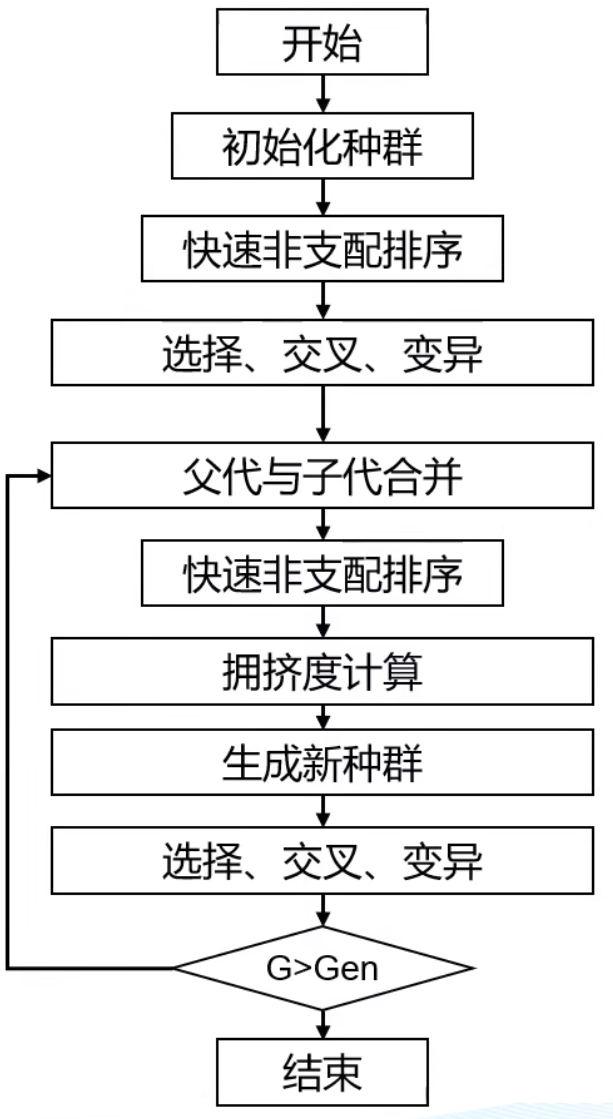
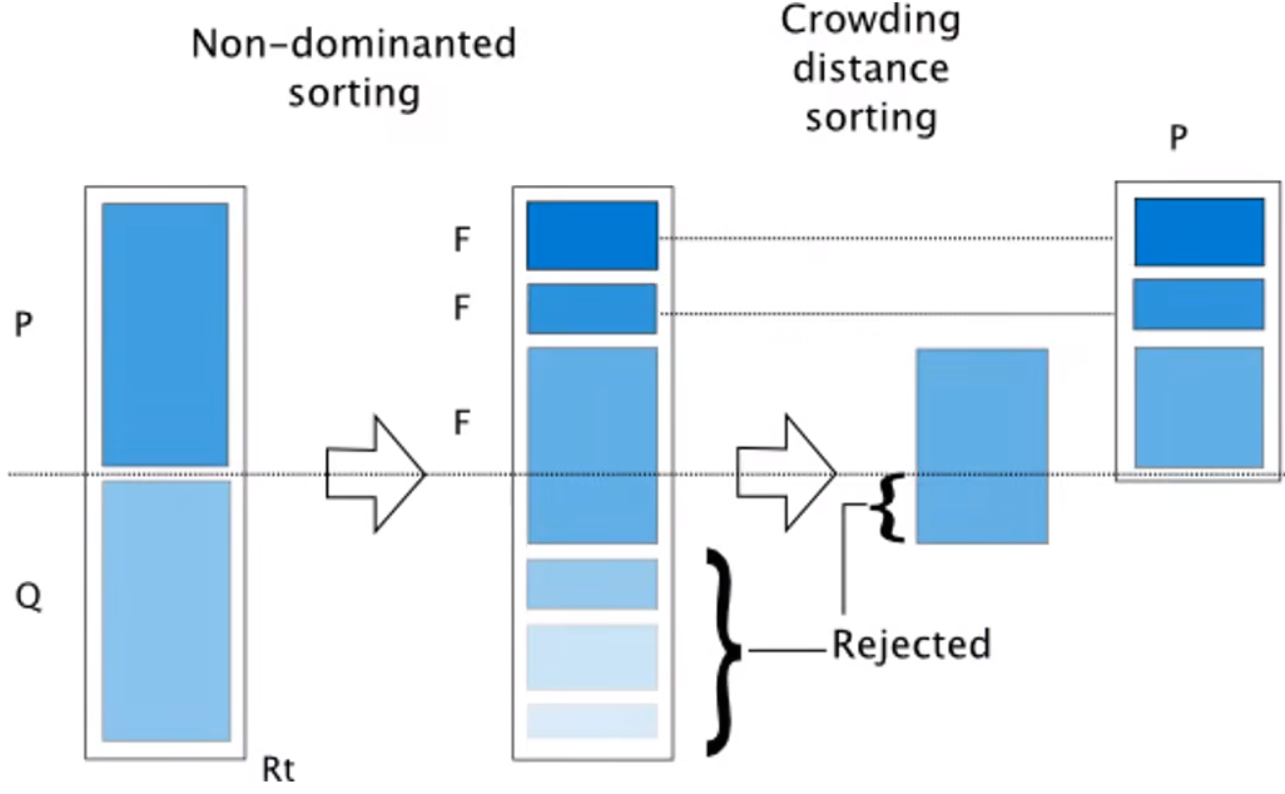
image-20220626144242472 image-20220626144417990

和单目标相似,但多了快速非支配排序(右图,用于决定哪个解好).

P是父代,P通过交叉变异生成子代Q,然后判断支配关系,得到多个序列前沿(得先去掉之前的前沿才能找下一个)

然后按照序列大小保留个体,如果前沿个体太多,不能全部保留(如图中第三个F),要么随机淘汰,要么根据拥挤距离淘汰(距离小的淘汰)