在常见的一些任务上惊人地强

Multi-surrogate multi-tasking optimization of expensive problems(MS-MTO)

昂贵问题的多代理多任务优化,论文建议训练两个代理模型,一个是使用所有可用数据训练的全局代理模型,另一个是只使用部分数据训练的局部代理模型

所有使用真实目标函数评估的解都保存在一个存档/档案Arc中。然后,使用Arc中的所有数据将一个代理模型训练成全局模型(M_g),以协助探索整个搜索空间。另一个代理模型在Arc中具有最佳适应度的样本上进行训练,成为一个局部代理模型(M_l),以协助对局部区域的开发,这有望在一个有前途的子区域内近似原始函数。

**将全局和局部代理模型视为两个任务,将多代理模型引入MFEA.然而,我们不能保证两个不同的代理模型有相似的最优解,即使它们是在同一原始问题的数据上训练出来的。因此,这项工作采用了广义多因子进化算法(G-MFEA)**作为搜索方法,它能够更有效地解决最优解不在同一区域或搜索维度不同的多个任务。

在MS-MTO中,探索和开发是通过同时优化全局和局部代理模型作为两个不同但相关的任务来进行的,这与传统SAEAs不同

算法流程

代理模型使用RBF,激活函数是立方(cubic)函数 $\phi\left(\left\|\mathbf{x}-\mathbf{c}_{i}\right\|\right)=\left(\left\|\mathbf{x}-\mathbf{c}_{i}\right\|\right)^{3}$

1. 使用拉丁超立方体抽样(LHS)生成N_I个解决方案,使用真实的目标函数进行评估这些解决方案,并保存在一个存档Arc中

2. 进行下面的循环,直到计算预算用尽,即达到允许的最大适应度评价数量:

3. 使用Arc中的所有数据训练一个全局代理模型(M_g);使用Arc中具有最佳适应度(要排序)的样本上训练一个局部代理模型(M_l)

4. 确定用在多任务优化上的交配概率(下面有提到)

5. 根据算法2(G-MFEA小改),找到两个代理模型的目前最优解

6. 使用真实的目标函数进行评估上面两个解,以便在下一轮更新两个RBF代理模型

7. 把这两个解保存到Arc

输出Arc的最好解

Arc中的初始样本数量不应过大或过小。如果初始样本的数量太大,计算资源将被浪费,而如果数据太小,代理模型的质量将太差,无法发挥作用。因此,N_I将被设定为训练局部代理模型所需的数据数量,假设训练局部代理模型所需的数据数量通常不超过训练全局模型的数据数量。

一个例子

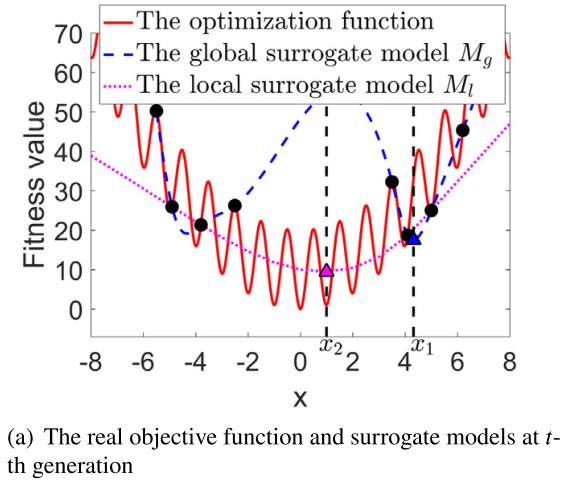
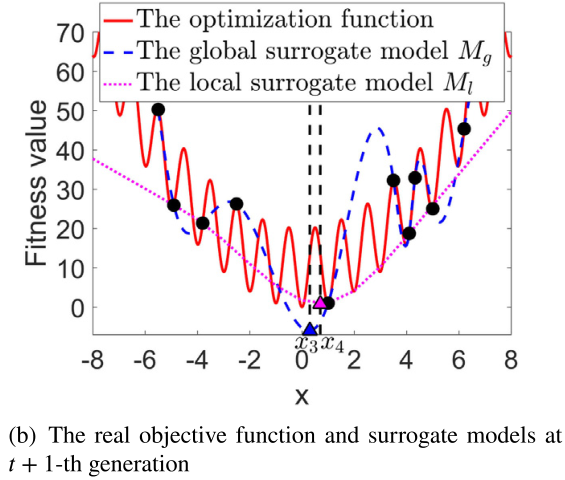
图1给出了一个说明性的例子,以显示本工作中全局和局部代理模型的贡献。假设在第t代的存档中有8个样本(图1(a)中的黑点)。所有这些样本都被用来训练全局代理模型M_g(用蓝色虚线表示)。而局部代理模型M_l(用粉色虚线表示)是用四个具有最佳适应度的样本来训练的。假设到目前为止发现的Mg和Ml的最佳解决方案分别是x1和x2

那么这两个解决方案将使用真实的目标函数进行评估,并保存在档案中,以便在下一代更新两个代理模型Mg和Ml。图1(b)显示了在上一代评估了x1和x2后,在第t+1代更新的全局和局部代理模型.我们可以看到,全局代理模型Mg的最优解,表示为x3,现在更接近于实际目标问题的最优解,这是由之前的局部代理模型找到的解x2贡献的。在这个例子中,到目前为止在第t代发现的全局代理模型的最佳解并没有对局部代理模型的更新做出贡献,因为它不包括在局部代理模型的训练数据中。总之,更新后的本地代理模型可以更好地捕捉到真实目标函数的分布

交配概率(交叉概率μ,变异概率σ)

交配概率被用来平衡多任务优化中搜索的探索和利用。一个小的交配概率意味着强调对搜索空间有限区域的利用,一个大的交配概率将促进对整个搜索空间的探索。

在所提出的MS-MTO方法的初始阶段,两个代理模型的最优解可能有很大差异,因为用于训练局部代理模型的数据分布在整个决策空间。因此,在第一阶段应使用小的交配概率来利用局部区域。

随着评估找到的全局和局部代理模型的最优解,训练数据将会增加,可用于训练局部代理模型的数据将分布在搜索空间的一个子区域。因此,在这个子区域中,局部模型的分布将与全局模型的分布更加相似,使得搜索更有可能陷于局部最优。这时候我们建议扩大交配概率,以帮助摆脱局部最优。

听起来像动态的rmp

交配概率选择

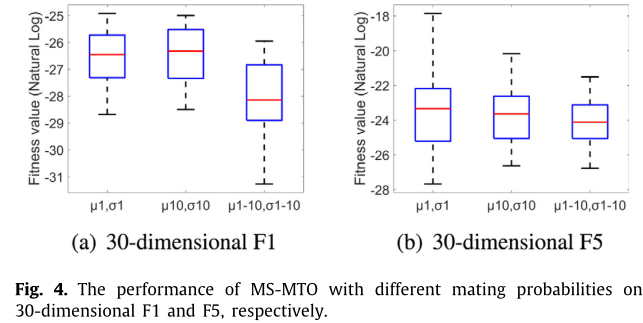
µ和σ分别代表交叉和变异的概率。µ1,σ1表示对于每个多任务优化,交叉(µ)和突变(σ)设置为1。µ1-10,σ1-10表示交叉和突变的概率从1变为10,其值=(MTO_calls/10 + 1),其中MTO_calls是迄今为止多任务优化的总调用数。从图4中,我们可以清楚地看到,交配概率线性增加的方法可以获得比其他交叉和变异概率固定的方法更好的性能。

全局和局部的多任务优化

全局和局部代理模型一起是否能更好地促进找到原始问题的最优解,取决于两个代理模型的分布,这又在很大程度上取决于训练数据集。多任务优化已被证明可以提高搜索性能,特别是当不同的任务在其适应度分布中具有相似的特征时。

算法2给出了在两个代理模型上进行优化的多任务优化算法的伪代码。在这项工作中没有使用G-MFEA中提出的洗牌(shuffling)技术

输入:全局代理模型M_g,局部代理模型M_l,最大迭代次数Kmax,交叉概率μ,变异概率σ

输出:两个代理模型的最优解

1. 生成一个具有N_P个体的初始种群P。注意这里有个历史数据选择策略,要从Arc中选一些历史解决方案放到初始种群中,用来帮助探索与当前最优解决方案所在区域不同的区域。
2. 初始种群P中的所有个体将分别使用全局和局部代理模型进行评估
3. 计算种群中每个个体的技能因子(根据每个任务的因子排名来确定)
4. 当停止标准(达到预先定义的最大迭代次数)没有达到时,将重复以下步骤:
5. 每个个体通过决策变量翻译策略被映射到一个新的位置
6. 与MFEA类似,通过同种交配策略产生一个子代种群C
7. 子代种群C通过决策变量翻译策略翻译回去
8. 子代种群C中的每个个体将根据垂直文化传播被分配一个技能因子
9. 并在相应的任务(两个代理模型中的一个)上进行评估
10. P和C拼接成中间种群R
11. 更新R中的标量适应度
12. 从R中选择下一代种群P

输出两个代理模型的最优解

历史数据选择策略

当多任务优化开始寻找两个任务的最优解,即更新的全局和局部代理模型时,首先会产生一个新的初始群体。为了找到比目前发现的计算成本高的问题的最佳解决方案,Arc中的一些历史解决方案将被包括在初始化群体中,这些解决方案已经使用真正昂贵的函数进行了评估。我们对历史数据的选择进行了五种不同的策略,即HD0、HD25、HD50、HD100和HD25-1。假设NP是种群规模,HD0、HD25、HD50和HD100分别表示初始种群的N_P解决方案的0%、25%、50%和100%将从档案Arc中复制,其中的解决方案按升序排序(从好到坏)。也就是说,档案中最好的解决方案将被用于初始化部分群体。HD25-1与HD25不同,它首先从Arc档案中挑选出50%N_P的最佳解(相当于HD50),然后随机选择这些解中的一半复制到初始种群中。这保证了初始种群总是包含迄今为止发现的最佳解决方案。

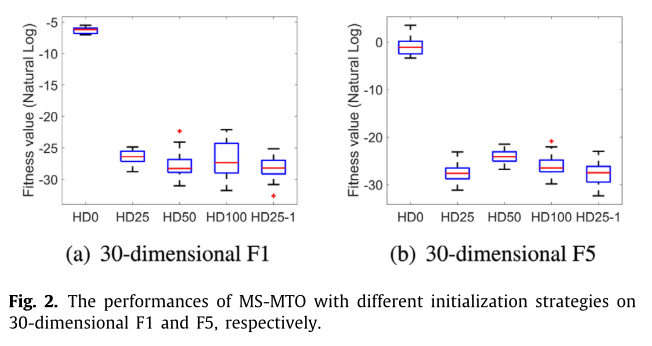
初始群体中包含历史数据的方法的性能要比没有数据的方法好得多。此外,HD25-1相对稳定,可以分别获得比HD25、HD50和HD100更好的结果

决策变量翻译策略

决策变量翻译策略将个体的解映射到一个新的空间,其中所有任务的最优解都位于同一位置,可以在增强种群多样性和加速种群收敛之间保持更好的平衡

详情去看G-MFEA论文.简单来说就是同种交配前把各决策变量加减一下,交配得到子代后,子代把自己的各决策变量加减回去

实验

从所提出的MS-MTO算法的详细描述中,我们可以看出MS-MTO算法的性能主要依赖于三个部分：用于优化两个任务的初始群体P,即全局和局部代理模型；多任务算法优化两个任务的停止准则；交配概率。

我们对30维Ellipsoid和Rastrigin问题进行了试验研究,这两个问题分别是单模态和多模态的,以确定合适的参数设置。然后,我们分析了所提算法的搜索动态和计算复杂性。接下来,为了考察多任务优化的贡献,我们还对12个分别具有10、20、30、50、100和200维的测试问题进行了比较研究。最后,我们提出的MS-MTO算法得到的实验结果将与最近提出的一些处理计算量大的问题的方法进行比较,包括CAL-SAPSO[40]、GORS-SLPSO[30]、SHPSO[38]、SA-COSO[37]、MGP-SLPSO[25]和SAMSO[31],以评价我们提出的方法在低维和高维问题上的性能。

总结

使用代理技术解决计算成本高的问题仍然具有挑战性,特别是当维度变得很高时。本文提出构建一个全局和一个局部的代理,通过多任务优化方法一起解决这些问题。然后,在开始新一轮的多任务优化之前,使用真实的目标函数对发现的最优值进行评估,并将其添加到档案中,以更新全局和局部代理指标。此外,在优化过程中对多任务优化的交配概率进行调整,以控制知识转移的程度。实验结果表明,所提出的算法在低维和高维问题上都优于本工作中研究的最先进的算法。

据我们所知,这是第一次尝试建立两个代理模型并使用进化多任务优化来搜索这两个代理模型。很容易想象,可以使用不同的训练数据训练更多的代理模型来进一步提高搜索效率,其中促进多个代理模型多样性的有效方法可能是至关重要的。此外,如何开发新的算法来寻找一个具有狭窄山谷的多模型问题的良好解决方案仍然是一项具有挑战性的任务。